Q. Signed 1s complement representation?

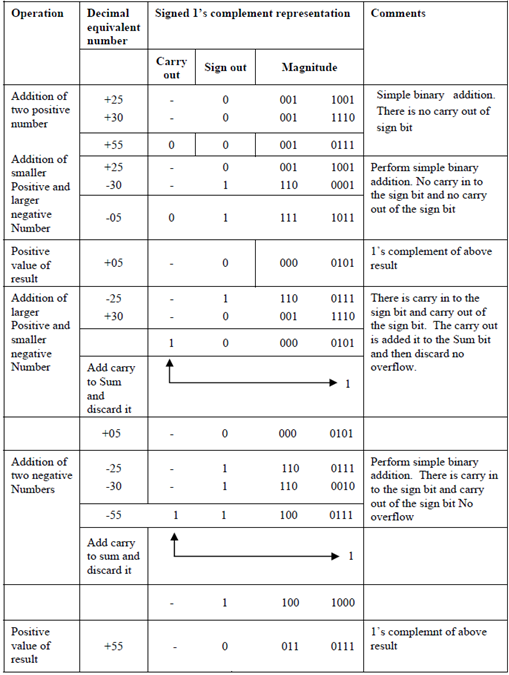
Another possibility that is also simple is use of signed 1's complement. Signed 1's complement has a principal. Add both numbers including sign bit. If carry of most significant bit or sign bit is one then increment result by 1 and discard carry over. Let's repeat all operations with 1's complement.

Another interesting characteristic about these representations is representation of 0. In 1's complement and signed magnitude there are two representations for zero as:

Representation                                            + 0                                            -0  

Signed magnitude                         0       000 0000   1                             000 0000  

Signed 1's complement                0       000 0000   1                             111 1111 

However in signed 2's complement there is only one zero and there is no negative or positive zero.

So -0 in 2's complement notation is similar like +0 and is equivalent to 0 000 0000. So both +0 and -0 are similar in 2's complement notation. This is an extra benefit in favour of 2's complement notation.

Highest number which can be accommodated in a register also relies on type of representation. In general in an 8 bit register 1 bit is used as sign so rest 7 bits can be used for representing value. The highest and lowest numbers which can be represented are:

For signed magnitude representation   (2⁷ - 1) to - (2⁷ - 1)  

  = (128-1) to   - (128- 1)  

  = 127 to -127  

For signed 1's complement     127 to -127

Although for signed 2's complement we may represent +127 to -128. The - 128 is signified in signed 2's complement notation as 10000000.