Q. Show Trigonometric Functions on a Graph?

Ans.

By discussing the trig functions with respect to an angle in a right-angle triangle, we have only considered angles between 0^o and 90^o. What about angles of 90^o and larger?

For simplicity, lets concentrate on the unit circle. When the angle is between zero and ninety degrees, we can use a triangle to help us find sine, cosine and tangent of the angle.

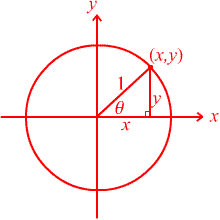
From this diagram, you can see that sinθ = y , cosθ = x and tan θ = y/x when 0^o< θ<90^o or 0 < θ < Π.

We can use everything we know about angles between 0 and Π/2 , to find the values of sine, cosine and tangent of ALL angles! 
(Remember that we are only dealing with points on the unit circle at the moment!)

Let's consider all four quadrants of the Cartesian plane.

First consider the second quadrant with angles between 90^o and 180^o.

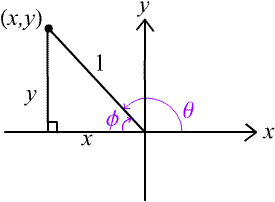
The angles θ and Φ are related as follows:

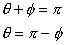
Since 0^o < Φ < 90^o we can use a right-angle triangle to find sinΦ.

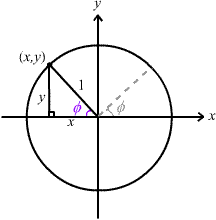
sinΦ = y , cosΦ = x and tanΦ = y/x BUT notice that in this quadrant, x is negative! Thus cos Φ and tan Φ are both negative, but sin Φ is positive.

This is all well and good, but why are we looking at sin Φ when all we want to know is sinθ ?WHY?

Thus sin θ = sin(Π -θ), cos θ = -cos (Π -θ) and tan θ = -tan (Π -θ)

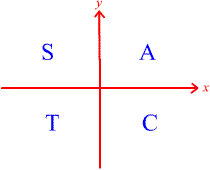
In fact, aside from the first quadrant, all the other quadrants have only one of sine, cosine or tangent positive.

sin θ is positive in the second quadrant.

tan θ is positive in the third quadrant.

cos θ is positive in the fourth quadrant.

Although we restricted ourselves to all the points on the unit circle, the trigonometric functions are dependent purely on the angle. Thus we now know the sine, cosine and tangent of every angle

The following picture shows which functions are positive in the four quadrants.

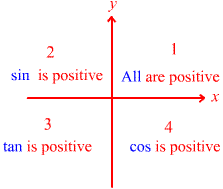
Here is a simple way to help you remember this information. Write the word CAST counter-clockwise beginning in the fourth quadrant. These letters symbolize which functions are positive.