Example Show that p ( x ) = 2 x3 - 5x2 -10 x + 5 has a root somewhere in the interval [-1,2].
Solution What we're actually asking here is whether or not the function will take on the value
p ( x ) = 0
somewhere among -1 and 2. In other terms, we desire to show that there is a number c such that -1 < c < 2 and p (c ) = 0 . Though if we described M = 0 and acknowledge that a = -1 and b = 2 we can distinguish that these two condition on c are precisely the conclusions of the Intermediate Value Theorem.
Thus, this problem is set up to employ the Intermediate Value Theorem and actually, all we need to do is to illustrates that the function is continuous and that M = 0 is among p ( -1) and p ( 2) (that means p ( -1) < 0 < p ( 2) or p (2) < 0 < p (-1) and we'll be done.
To do this all we have to do is compute,
p ( -1) = 8 p ( 2) = -19
Hence, we have,
-19 = p ( 2) < 0 < p ( -1) = 8
Therefore M = 0 is among p ( -1) and p ( 2) and as p ( x ) is a polynomial it's continuous everywhere and thus particularly it's continuous on the interval [-1,2]. Thus by the Intermediate Value Theorem there has to be a number -1 < c < 2 so that,
p (c ) = 0
Thus the polynomial does have a root among -1 & 2.
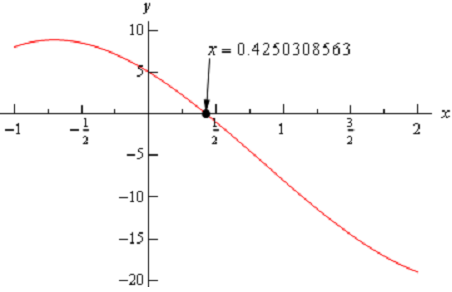
For the sake of completeness here is a graph illustrating the root that just we proved existed. Note as well that we utilized a computer program to in fact find the root and that the Intermediate Value
Theorem did not tell us what this value was.