In figure, the incircle of triangle ABC touches the sides BC, CA, and AB at D, E, and F respectively. Show that AF+BD+CE=AE+BF+CD= 1/2 (perimeter of triangle ABC),
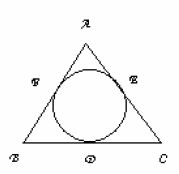
Ans: Since the length of tangents from an external point to are equal
∴AF = AE
FB = BD
EC = CD
Perimeter of ΔABC = AB + BC+ AC
= AF + FB + BD + DC + AE + EC
= AF + BD + BD + CE + AF + CE (Θ AF=AE, FB=BD, EC=CD)
= AF + AF + BD + BD + CE + CE
Perimeter of ΔABC = 2(AF + BD+ CE)
∴AF + BD + CE =
1/2 (perimeter of ΔABC) ........(1)
Perimeter of ?ABC = AB + BC + AC
= AF + FB + BD + DC + AE + EC
= AE + BF + BF + CD + AE + CD (Θ AF = AE, FB = BD, EC = CD)
= AE + AE + BF + BF + CD + CD
Perimeter of ΔABC = 2(AE + BF + CD)
∴AE + BF + CD =
1/2 (perimeter of ΔABC) ........(2)
From (1) and (2)
AF + BD + CE = AE + BF + CD = 1/2 (perimeter of ΔABC)