Q. Show Basic concepts of permutation?

Let us look at the basic concepts of permutation with respect to interconnection network.  Let us say the network has set of n input nodes and n output nodes.

Permutation P for a network of 5 nodes (i.e., n = 5) is written like this:

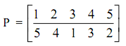
It signifies node connections are 1↔5, 2↔4, 3↔1, 4↔3, 5↔2.

The connections are displayed in the Figure below.  

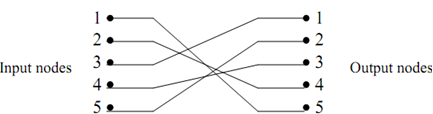
Figure: Node-Connections

The other permutation of the similar set of nodes can be 

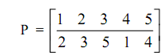
That means connections are: 1↔2, 2↔3, 3↔5, 4↔1, and 5↔4 similarly other permutations are also possible.  The set of all permutations of a 3 node network would be 

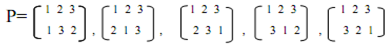
Connection, signifies connection from node 1 to node 1, node 2 to node 2, and node 3 to node 3 therefore it hasn't any meaning, so it's dropped. In these illustrations, only one set of links exist between output and input nodes and denotes it's a single stage network.  It might be probable that there exist many links between input and output (It means that multistage network).  Permutation of all these in a multistage network are known as permutation group and these stand for by a cycle for example permutation.

P= (1,2,3) (4,5) means that the network has two sets of input and output nodes, one group contains nodes 1,2,3 and another group contains nodes 4,5 and associations are 1→2, 2→3, 3→1, and 4→5. Here set (1, 2, 3) has period 3 and (4, 5) has period 2, Together these groups has periodicity 3×2=6. 

Interconnection from all the probable input nodes to all output nodes structures the permutation group.

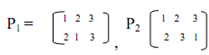
The permutations can be joined. This is known as composition operation. In composition operation two or more permutations are concerned in sequence, for example if P₁ and P₂ are two permutations stated like this:

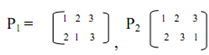
The composition of P₁ and P₂ will be

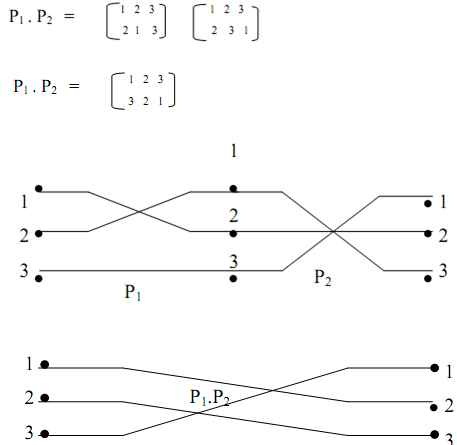
Similarly,

If P₃ = 

And P₄ =

Then P₃. P₄ =

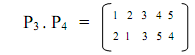
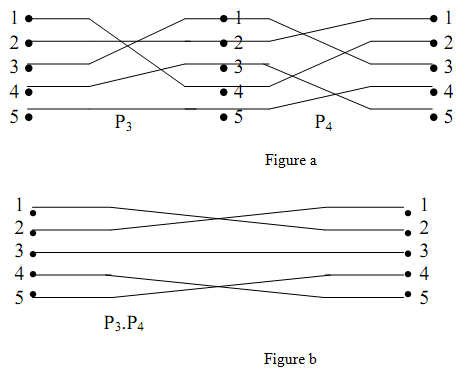
Compositions of those permutations P₁ and P₂ are represented in Figures a and b.