Before we find into finding series solutions to differential equations we require determining when we can get series solutions to differential equations. Therefore, let's start with the differential equation,

 p (x) y′′ + q (x) y′ + r (x )y = 0                   (1)

Now there we really do mean nonconstant coefficients. For this point we've only dealt along with constant coefficients. Though, with series solutions we can now contain nonconstant coefficient differential equations. As well as, in order to make the problems some nicer we will be dealing only along with polynomial coefficients.

Here, we say that x=x₀ is an ordinary point if given both,

q(x)/p(x)                      and                  r(x)/p(x)

Both are analytic at x=x₀. It is to say that such two quantities have Taylor series around x=x₀. Our aim is only dealing with coefficients which are polynomials thus this will be equivalent to saying as,

p(x₀) ≠ 0

If a point is not an ordinary point so we call this a singular point.

The fundamental idea to finding a series solution to a differential equation is to suppose that we can write the solution like a power series in the form,

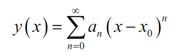..................(2)

And then try to find out what the a_n's require to be. We will only be capable to do this if the point x=x₀, is an ordinary point. We will generally say as (2) is a series solution around x=x₀.

Let's begin with a very fundamental example of this. Actually this will be so fundamental that we will contain constant coefficients. It will permit us to check that we find the exact solution.