Rules of Integration
1. If 'k' is a constant then
2. In the above rule, if k = 1 then
| ∫dx |
(this means integral of 1 which is written as dx and not 1 dx) |
= x + c
3.
| ∫xndx |
= |
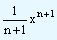 |
+ c |
*
|
- 1 |
The integral of 1/x or x-1 is
The condition x > 0 is added because only positive numbers have logarithms.
4.
| ∫akxdx |
= |
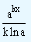 |
+ c where 'a' and 'k' are constants.
|
5.
| ∫eKxdx |
= |
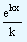 |
+ c since ln e = 1 |
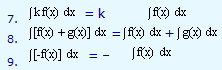
Functions which differ from each other only by a constant have the same derivative. For example, the function F(x) = 4x + k has the same derivative, F'(x)= 4 = f(x), say, for any infinite number of possible values for k. If the process is reversed, it is clear that ∫4dx is the indefinite integral for an infinite number of functions differing from each other only by a constant. The constant of integration, mentioned 'c' in the expression for integration earlier, thus represents the value of any constant which was part of the original function but precluded from the derivative by the rules of differentiation.
The graph of an indefinite integral ∫f(x)dx = F(x) + c, where 'c' is unspecified, is a family of curves parallel in the sense that the slope of the tangent to any of them at x is f(x). Specifying 'c' gives a single curve whereas changing 'c' shifts the curve vertically. If c = 0, the curve begins at the origin.
For example, ∫4d(x) = 4x + c. For c = -7, -3, 0, 1 and 4 the graph of this integral is given below.
Figure