Rotation - 2-d and 3-d transformations

Given a 2-D point P(x,y), that we want to rotate, along with respect to an arbitrary point A(h,k). Suppose P'(x'y') be the effect of anticlockwise rotation of point P via angle q about A, that is demonstrated in Figure 6.

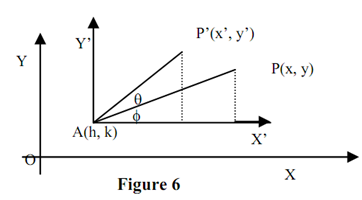
Because, the rotation matrix R_q is explained only with respect to the origin, we have a set of fundamental transformations, that constitutes the composite transformation to calculate the rotation regarding a given arbitrary point A, signified by R_q,A. We can find out the transformation R_q,A in three steps:

Translate the point A(h,k) to the origin O, hence the center of rotation A is at the origin.

Execute the necessary rotation of q degrees about the origin, and also

Translate the origin back to the original position A(h,k).     

Using v=hI+kJ as the translation vector, we have the following sequence of  three transformations:

R_q,A =T_-v. R_q. T_v