Q. Resultant air-gap flux of induction machine?

The resultant air-gap flux is produced by the combined mmfs of the stator and rotor currents. For the sake of conceptual and analytical convenience, the total flux is divided into a mutual flux (linking both the stator and the rotor) and leakage fluxes, represented by appropriate reactances.

Considering the conditions in the stator, the synchronously rotating air-gap wave generates balanced polyphase counter emfs in the phases of the stator. The volt-ampere equation for the phase under consideration in phasor notation is given by

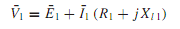
where ¯ V₁ is the stator terminal voltage, ¯ E1 is the counter emf generated by the resultant air-gap flux, ¯I₁ is the stator current, R₁ is the stator effective resistance, and Xl₁ is the stator-leakage reactance.

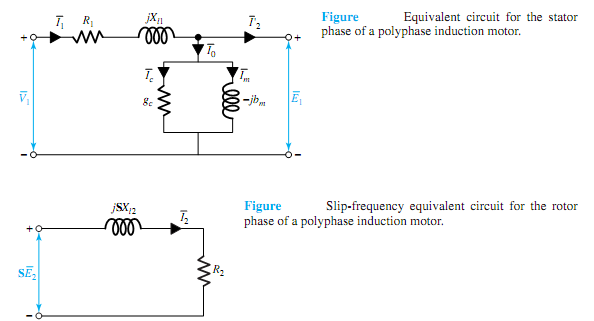
As in a transformer, the stator (primary) current can be resolved into two components: a load component ¯I₂ (which produces an mmf that exactly counteracts the mmf of the rotor current) and an excitation component ¯I₀ (required to create the resultant air-gap flux). This excitation component itself can be resolved into a core-loss component ¯ I_c in phase with ¯E₁

and a magnetizing component ¯I_m lagging ¯E₁ by 90°. A shunt branch formed by the core-loss conductance g_c and magnetizing susceptance bm in parallel, connected across ¯E₁, will account for the exciting current in the equivalent circuit, as shown in Figure, along with the positive directions in a motor.