Responses to Exponential Excitations

Let us consider Aest as a typical exponential excitation in which A is a constant and s is a complex- frequency variablewith a dimension of 1/second such that the exponent st becomes dimensionless.

The variable s can assume real, imaginary, or complex values. The time-invariant dc source is represented by setting s = 0. The use of s = jω would imply sinusoidal excitation.

Note that Aest is the only function for which a linear combination of

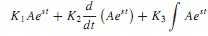
in which K₁, K₂, and K₃ are constants has the same shape or waveform as the original signal. Therefore, if the excitation to a linear system is Aest, then the response will have the same waveform.

Recall the volt-ampere relationships (for ideal elements) with time-varying excitation.

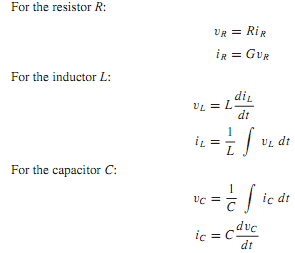
With exponential excitation in which v(t) = V_est and i(t) = I_est, it can be seen that the following holds good because exponential excitations produce exponential responses with the same exponents. (Notationwise, note that v(t) and i(t) represent the real-valued signals, whereas v(t) and i(t) represent complex-valued signals.)

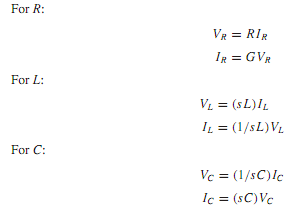
The preceding equations resemble the Ohm's law relation. The quantities R, s_L, and 1/s_C have the dimension of ohms, whereas G,1/s_L, and sC have the dimension of siemens, or 1/ohm. The ratio of voltage to current in the frequency domain at a pair of terminals is known as the impedance, designated by Z(s), whereas that of current to voltage is called the admittance, designated by Y(s). Note that both the impedance and the admittance are in general functions of the variable s, and they are reciprocal of each other. Such expressions as Equations 15 through 16 relate the amplitudes of the exponential voltages and currents, and are the frequency-domain representations of the elements. Networks drawn using impedance or admittance symbols are known as transformed networks, which play a significant role in finding the network response, as shown in the following examples.