It is the last case that we require to take a look at. During this section we are going to look at solutions to the system,

x?' = A x?

Here the eigenvalues are repeated eigenvalues. As we are going to be working with systems wherein A is a 2x2 matrix we will create this assumption from the start. Therefore the system will have a double eigenvalue, l.

It presents us with a problem. We need two linearly independent solutions hence we can form a general solution. Though, with a double eigenvalue we will have only one,

x? = ?h e^lt

Therefore, we need to come up along with a second solution. Recall this when we looked at the double root case along with the second order differential equations we ran in a same problem. In those sections we simply added a t to the solution and were capable to get a second solution. Let's notice if similar thing will work into this case as well.  We'll notice if,

x? = t e^lt  ?h

It will also be a solution.

To check all we want to do is plug in the system.  Keep in mind to product rule the proposed solution while you differentiate!

?h e^lt+ l t e^lt  ?h = A t e^lt  ?h

Here, we got two functions this time on the left side, an exponential through itself and exponential times a t. Therefore, in order for our guess to be a solution we will require to need,

A ?h=l ?h           ⇒         (A - lI) ?h= ?0

?h = ?0

The first requirement isn't a problem as this just says as l is an eigenvalue and its eigenvector is ?h. We already identified this therefore there's nothing new there. The second though is a problem. As ?h is an eigenvector we know that this can't be zero, even in order to satisfy the second condition this would have to be.

Therefore, our guess was incorrect.  The problem appears to be that there is a lone term with just an exponential into it ?hlet's see if we can't fix up our guess to accurate that. Let's try the subsequent guess.

x? = t e^lt  ?h +  e^lt?r

Here ?ris an unknown vector which we'll need to find out.

As with the first guess here we plug this in the system and notice what we get.

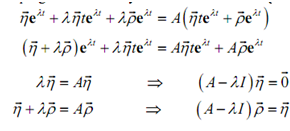
Above is again set coefficients equal is shown.

As along with our first guess the first equation gives us nothing which we didn't already know. Now there the second equation is not a problem. Each the second equation gives us that ?r must be a solution to that equation.

It seems our second guess worked. So,

x? ₂= t e^lt  ?h +  e^lt?r

It will be a solution to the system provided ?r  is a solution to;

(A - lI) ?r =  ?h

Also above solution and the first solution are linearly independent and therefore they form a fundamental set of solutions and therefore the general solution in the double eigen-value case is,

x?(t) = c₁ e^l₁^t  ?h + c₂ (le^l₂^t  ?h+  e^lt?r)