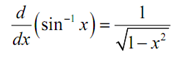Relationship between the inverse sine function and the sine function

We have the given relationship among the inverse sine function and the sine function.

                   sin (sin ^-1 x ) = x                                     sin ^-1 (sin x ) =x

In other terms they are inverses of each other. it means that we can utilizes the fact above to determine the derivative of inverse sine.  Let's start with,

f ( x ) = sin x                                                g ( x )= sin ^-1 x

Then,

g′ ( x ) = 1/ f ′ ( g ( x )) =         1 /cos (sin ^-1  x )

It is not an extremely useful formula.  Let's see if we can obtain better formula.  Let's begin by recalling the definition of inverse sine function.

                                          y ( sin ^-1 ( x )         ⇒ x = sin ( y )

By using the first part of this definition the denominator into the derivative becomes,

                                                 cos (sin ^-1 x ) = cos ( y )

Now, recall that

cos²  y + sin ²  y =1      ⇒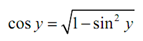 

By using this, now the denominator is,

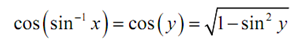
Now, utilizes the second part of the definition of the inverse sine function. Then the denominator is,

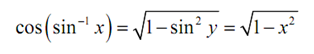
Putting all this together gives the given derivative.