Rate of Change : The first interpretation of derivative is rate of change. It was not the primary problem which we looked at in the limit chapter, however it is the most significant interpretation of the derivative. If f ( x ) represents a quantity at any x then the derivative f ′ ( a ) represents the instantaneous rate of change of f ( x )at x = a .
Example Assume that the amount of water into a holding tank at t minutes is provided by
V (t ) = 2t 2 -16t + 35 . Find out each of the following.
(a) At t = 1 minute is the volume of water within the tank increasing or decreasing?
(b) At t = 5 minutes is the volume of water within the tank increasing or decreasing?
(c) Is the volume of water within the tank changing faster at t = 1 or t = 5 minutes?
(d) Is the volume of water within tank ever not changing? If so, when?
Solution
In this instance we will utilizes both of the notations for the derivative simply to get you familiar along with the different notations.
We will require the rate of change of the volume to answer these questions. It means that we will require the derivative of this function as that will give us a formula for rate of change at any time t
The derivative is.
V ′ (t ) = 4t -16 OR dV/ dt = 4t -16
If rate of change was +ve then the quantity was increasing and if the rate of change was negative then it was decreasing.
Now we can work the problem.
(a) Is the volume of water in the tank increasing or decreasing at t = 1minute?
In this case all that we require is the rate of change of the volume at t = 1or,
V ′ (1) = -12 OR
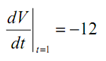
Hence, at t = 1 the rate of change is negative and therefore the volume have to be decreasing at this time.
(b) Is the volume of water inside the tank increasing or decreasing at t = 5 minutes?
Again, we will require the rate of change at t =5 .
V ′ (5) = 4 OR
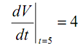
In this the rate of change is positive & hence the volume have to be increasing at t = 5 .
(c) Is the volume of water inside the tank changing faster at t = 1 or t = 5 minutes?
To solve out this question all that we look at is the size of rate of change & we don't worry regarding the sign of the rate of change. All that we have to know here is that the larger the number the faster the rate of change. Thus, in this case the volume is changing faster at t = 1 than at t = 5 .
(d) Is the volume of water inside the tank ever not changing? If so, then when?
The volume will not be changing if it has rate of change of zero. In order to contain a rate of change of zero it means that the derivative has to be zero. Thus, to solve this question we will then have to solve out
V ′ (t ) = 0 OR dV/ dt = 0
It is easy enough to do.
4t -16 = 0 ⇒ t = 4
Thus at t = 4 the volume isn't changing. Note as well that all this is saying is that for brief instant the volume isn't changing. This doesn't say that at this instance the volume will quit changing permanently.
If we go back to our answers from parts (a) & (b) we can get an idea regarding what is going on. At t = 1 the volume is decreasing and at t = 5 the volume is increasing. Therefore at some point in time the volume have to switch from decreasing to increasing. That time is t = 4 .
It is the time wherein the volume goes from decreasing to increasing and hence for the briefest instant in time the volume will quit changing as it changes from decreasing to increasing.