Two stations due south of a tower, which leans towards north are at distances 'a' and 'b' from its foot. If α and β be the elevations of the top of the tower from the situation, Prove that its inclination 'θ' to the horizontal given by
cotΘ = (bcot α - α cot β) / b-a
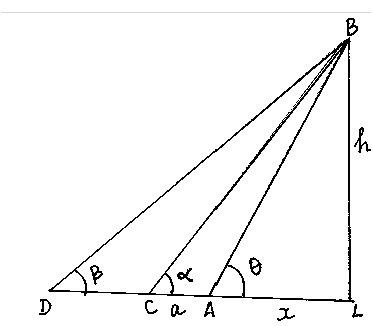
Ans: Let AB be the leaning tower and C and D be the given stations. Draw BL ⊥ DA produced.
Then, ∠BAL = 0, ∠BCA = α, ∠BDC = a and DA = b.
Let AL = x and BL = h
In right ΔALB, we have :
AL/BL = Cot θ ⇒ x/h = Cot θ
⇒ x/h = Cot θ ⇒ x = h cot θ .....(i)
In right ΔBCL, we have :
CL/BL = Cot α ⇒ a + x = h cot α
⇒ a = h (cot α - cot θ)
⇒ h =a / (cot α - cot θ) ...(ii)
In right ΔBDL, we have :
DL/BL = cot β ⇒ DA + AL/BL = cot β
⇒ b + x/h = cot β ⇒ b + x = b cot β
⇒ b = h ((cot β - cot θ) [using (i)]
⇒ h = b/(cot β - cotθ ) ...........(iii)
equating the value of h in (ii) and (iii), we get:
a/(cot α - cot θ )= b /(cot β - cotθ )
⇒ a cot β - a cot θ = b cot α - b cot θ
⇒ (b - a) cot θ = b cot α - a cotβ
⇒ cot θ = b cot α - a cot βθ/(b - a)