Proof of: lim_q→0 sinq/q = 1

This proofs of given limit uses the Squeeze Theorem. Though, getting things set up to utilize the Squeeze Theorem can be a somewhat complex geometric argument which can be difficult to follow therefore we will try to take this fairly slow.

Let's begin by assuming that 0 ≤ q ≤ p/2. Because we are proving a limit that has q → 0 it's fine to suppose that q is not too large that is q ≤ p/2.  Also, though assuming that q is positive we are really going to first proves that the given limit is true if this is the right-hand limit. Since you will see if we can prove it so the proof of the limit will be simple.

Therefore, now that we've found our assumption on q taken care of let's begin off with the unit circle circumscribed through an octagon along with a small slice marked out as demonstrated below.

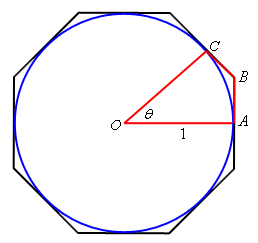
Points A and C are the midpoints as in shown above of their respective sides on the octagon and are actually tangent to the circle here. We will call the point where these two sides meet B.

By this figure we can notice that the circumference of the circle is less than the length of the octagon. It also means that if we consider the slice of the figure marked out above so the length of the portion of the circle contained in the slice should be less than the length of the portion of the octagon contained in the slice.

Since we're going to be doing most of our work on just the slice of the diagram let's strip that out and consider just this. There is a sketch of just the slice.

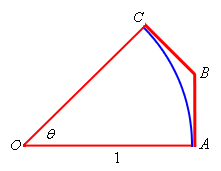
Here denote the portion of the circle through arc AC and the lengths of the two portion of the octagon shown by AB and BC. Then through the observation about lengths we complete above we should have,

 arc AC < |AB| + |BC|                                    (1)

Subsequently, extend the lines AB and OC as demonstrated below and call the point that they meet D. The triangle here formed through AOD is a right triangle. All this is demonstrated in the figure below.

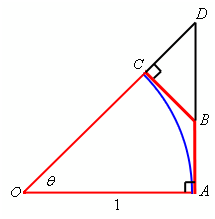
The triangle BCD is a right triangle along with hypotenuse BD and therefore we know |BC| < |BD|. Also consider that |AB| + |BD| = |AD|.  If we make use of these two facts in (1) we find,

arc AC < |AB| + |BC|

< |AB| + |BD|

= |AD|                                     (2)

Next, as noted previously the triangle AOD is a right triangle and therefore we can utilize a little right triangle trigonometry to write AS,

 |AD| = |AO| tanq.  Also note that |AO| = 1 since it is nothing more than the radius of the unit circle. Using this information in (2) gives,

 arc |AC| < |AD|

< |AO| tan q                          

 = tanq                                                 (3)

The subsequently thing which we require to recall is that the length of a portion of a circle is given through the radius of the circle times the angle which traces out the portion of the circle we are trying to measure. For our portion it means that,

 arc |AC| <  |AO|q = q

 Therefore, putting it in (3) we see that,

q = arc AC < tanq = sinq/cosq

Otherwise, if we do a bit rearranging we find

cosq < sinq/q                           (4)

We will be coming back to (4) in a little. Here we assume now add in a couple extra lines into our figure above. Let's join A and C with a line and drop a line straight down from C till this intersects AO at a right angle and here we call the intersection point E. it is all demonstrated in the figure as given below.

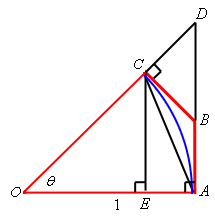
Okay, the primary thing to consider is as,

|CE| < |AC| < arcAC                                                   (5)

Also note that triangle EOC is a right triangle with a hypotenuse of triangle trig we can see that, |CO| = 1. By using some right

|CE| = |CO| sinq = sinq

Plugging it in (5) and recalling the arc AC = 0 we find,

sinq = |CE| < arc AC = q

and with a bit rewriting we find,

sinq/q < 1                                                        (6)

So, we're almost done at this point. Putting (4) and (6) mutually we consider that,

cosq <  sinq/q < 1

Given 0 < q < p /2.  Assume here that,

lim_q→0 cosq = 1                                                            lim_q→0 1 = 1                

We are here set up to use the Squeeze theorem. The only matter that we require to worry about is that we are staying to the right of q = 0 in our assumptions and therefore the best that the Squeeze Theorem define as,

lim_q→0 sinq/q = 1

Therefore, we know that the limit is true if we are only working along with a right-hand limit. Though we know that sin q is an odd function and thus,

Sin(-q)/(-q) = - (sinq)/(-q) = sinq/q

Conversely, if we approach zero from the left that is negative q's, then we will find similar values in the function like if we'd approached zero from the right that is positive q's and therefore,

lim_q→0¯  sinq/q = 1

We have now demonstrated that the two one-sided limits are similar and therefore we should also have,

lim_q→0 sinq/q = 1

It was a somewhat long proof and if you are not actually good at geometric arguments this can be type of confusing and daunting. Properly, the second limit is very easy to prove, provided you have previously proved the first limit.