Proof of Alternating Series Test

With no loss of generality we can assume that the series begins at n =1. If not we could change the proof below to meet the new starting place or we could perform an index shift to obtain the series to begin at n =1 .

First, notice that because the terms of the sequence are decreasing for any two successive terms we can say,

b_n - b_n+1 ≥ 0

Here now, let us take a look at the even partial sums.

s₂ = b₁ - b₂ ≥ 0

s₄ = b₁ - b₂ + b₃ - b₄ = s₂ + b₃ - b₄ ≥ s₂                                              because b₃ - b₄ > 0

S₆ = s4 + b5 - b6  ≥ s4                                                            because b₅ - b₆ > 0     

S_2n = S_{2n -2} + b_{2n -1} - b_2n  ≥ S_{2n -2}                                                           because b_2n-1 - b_2n > 0

Thus, {S_2n}is an increasing sequence.

 Next, we can as well write the general term as,

S_2n = b₁-b₂ + b₃ - b₄ + b₅ + .... - b_2n-2 + b_2n-1 - b_2n

= b₁ - (b₂-b₃) - (b₄ - b₅) + ..... - (b_2n-2 - b_2n-1) - b_2n

Every quantity in parenthesis is positive and by assumption we be familiar with that b_2n is as well positive.  Thus, this tells us that S_2n< b₁ for all n.

We now be familiar with that {S_2n}is an increasing sequence that is bounded above and thus we know that it must as well converge.  Thus, let's assume that its limit is s or,

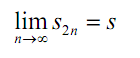
Subsequently, we can quickly find out the limit of the sequence of odd partial sums, {S_2n+1} as follows,

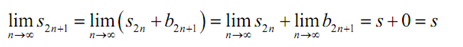
Thus, we now know that both of the {S_2n} and {S_2n+1} are convergent sequences and they both have similar limit and so we as well know that {S_n} is a convergent sequence along with a limit of s.  This in turn tells us that ∑a_n is convergent.