It can be geometrically proved that two elasticity are equal, which is., QB=RD Let's first consider ΔAOB. If we draw a horizontal line from point Q to intersect the vertical axis at point P and an ordinate from Q to M at the horizontal axis, we have 3 triangles- ΔAOB, ΔAPQ and ΔQMB. Note that ΔAOB, ΔAPQ and ΔQMB are right-angles. Thus, all the three triangles are right-angled triangles. As noted above, ratios of their two corresponding sides of similar right-angle triangles are always equal.

Considering only the relevant triangles, ΔAPQ and ΔQMB, we have

BQ/MQ =AQ/AP

Since MQ = OP, by substituting OP for QM in ratio BQ/MQ, we get

BQ/OP = AQ/AP

Therefore, BQ/AQ =OP/AP = Elasticity of demand curve AB, at point Q or at price OP.

We can similarly prove that

RD/RA = OP/PA = Elasticity of demand curve AD, at point R or at price OP.

Therefore it is proved, that at price OP,

QB/QA = RD/RA = PO/PA

It is hence proved that two demand curves with different slopes have the same elasticity at a given price.

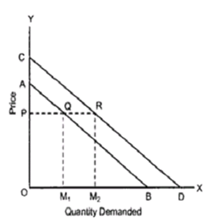
Price Elasticity of two parallel demand curves