The next topic that we desire to discuss here is powers of i. Let's just take a look at what occurring while we start looking at many powers of i.

i¹ = i                                                    i¹ = i

i²  = -1                                               i²  = -1

i³  =i ⋅ i²  = -i                                        i³  = -i

i⁴  = (i² )²  = ( -1)²  = 1                         i⁴ = 1

i⁵ = i ⋅ i⁴  = i                                          i⁵  = i

i⁶ = i² ⋅ i⁴  = ( -1) (1) = -1                    i⁶  =-1

i⁷ = i ⋅ i⁶  = -i                                        i⁷  = -i

i⁸  = (i⁴ )²  = (1)²  = 1                            i⁸  = 1

Can you notice the pattern?  All powers if i can be reduced down to one of four probable answers and they repeat every four powers continuously. It can be a convenient fact to remember.

Next we need to address an issue on dealing along with square roots of -ve numbers.  we know that we can do the following.

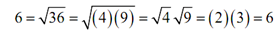
In other terms, we can break up products within a square root into a product of square roots provided both numbers are positive.

It turns out that actually we can do the same thing if one of the numbers is -ve.  For instance,

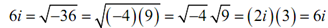
However, if both of numbers are negative it won't work anymore as the following shows.

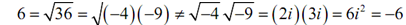
We can summarize it as a set of rules.  If a & b are both positive numbers then,

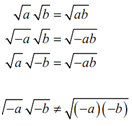
Consider the following example to know it's important.