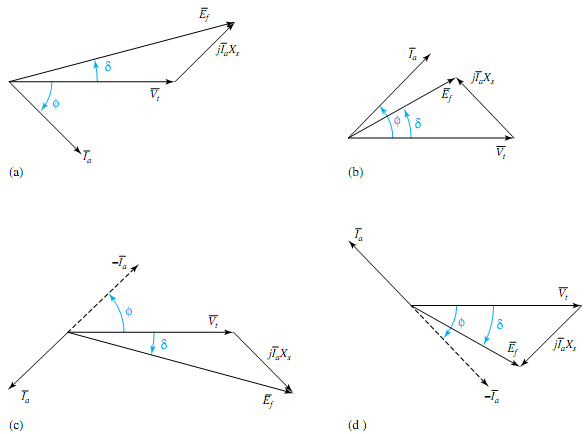
Q. Power Angle and Performance Characteristics?

The real and reactive power delivered by a synchronous generator, or received by a synchronous motor, can be expressed in terms of the terminal voltage V_t, the generated voltage E_f, the synchronous impedance Z_s, and the power angle or torque angle δ. Referring to Figure, it is convenient to adopt a convention that makes positive the real power P and the reactive power Q delivered by an overexcited generator. Accordingly, the generator action corresponds to positive values of δ, whereas the motor action corresponds to negative values of δ. With the adopted notation it follows that P > 0 for generator operation, whereas P< 0 for motor operation. Further, positiveQmeans delivering inductiveVARs for a generator action, or receiving inductive VARs for a motor action; negative Q means delivering capacitive VARs for a generator action, or receiving capacitive VARs for a motor action. It can be observed from Figure that the power factor is lagging when P and Q have the same sign, and leading when P and Q have opposite signs.

The complex power output of the generator in volt-amperes per phase is given by

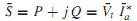
where ¯V_t is the terminal voltage per phase, ¯I_a is the armature current per phase, and * indicates a complex conjugate. Referring to Figure (a), in which the effect of armature resistance has been neglected, and taking the terminal voltage as reference, we have the terminal voltage,

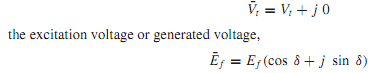
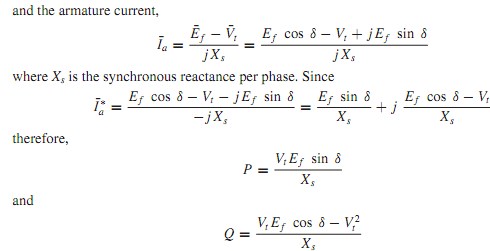
Equations hold for a cylindrical-rotor synchronous generatorwith negligible armature resistance. To obtain the total power for a three-phase generator, Equations should be multiplied by 3 when the voltages are line to neutral. If the line-to-line magnitudes are used for the voltages, however, these equations give the total three-phase power.