Suppose an interesting situation represented in following figure (b). The Petri net somewhat shows a paradoxical situation. Intuitively we contain in our minds that by raising the initial marking of the Petri net we can raise its chances of it being live. By sum a token to p₅ we can consider that t₂ can be fired and the system attains a deadlock.

Thus we can interpret that raising the number of resources or the initial markings not all times assists in making the system live.

Furthermore we ignore any potential deadlock by employing additional intermediate places. That type of deadlocks appear while the operation say O_{i, j, k} is completed in at the machine M_k and O_i,j+1,k1 needs the machine M_k1 and the operation O_i1,j1,k1 is done at machine M_k1 and O_{i1, j1+1,k} needs machine M_k. The situation is shown in following figure (a) as represented below.

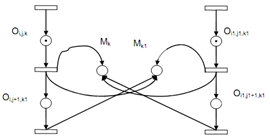
Figure: (a): A Potential Deadlock

The operations O_i,j+1,k and O_i1,j1+1,k1 are be reinitiated via swapping the resources M_k and M_k1. In the model represented in figure (a), the model fails to attain this. Hence we employ additional intermediate places to resolve the problem and it is portrayed in following figure (b) below.

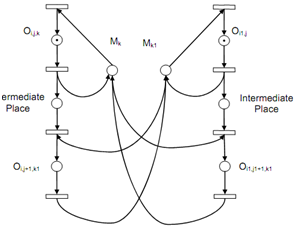
Figure: (b): A Solution for Potential Deadlock

The model as represented in figure consequent to having a buffer at machine. Via unloading otherwise via either a human operator or via a robot the part from the machine to the buffer after the operation the machine is available and deadlock does not arise. At all machine, the loading of the part onto the machine before the operation is seemed as the part of the operation. Such procedure avoids an exact type of potential deadlocks.