Positive Accelerations - Computer Animation

So as to incorporate increasing speed in an animation the time spacing among the frames should increase, hence greater change in the position arise, as the object moves faster. In common, the trigonometric function utilized to have raised interval size the function is (1- Cos Θ) ,0<Θ<Π/2 .

For n in-betweens, the time for the Jth in-between would be computed as:

ΔT_J = Ta + ΔT [1 - Cos( J (Π/ 2)( N + 1))];      J = 1, 2, 3,........, N

ΔT=time dissimilarity among two key frames =Tb-Ta

In above figure represents a positive acceleration case since the space (that is, time space) among frames continuously raising leading to the raise in accelerations that are changes in object position in two frames is fast. Here we study the trigonometric function utilized to find out positive acceleration, as Y=(1-Cos Θ) ,0<Θ<Π/2

 At Θ = 0;

Y = (1 - Cos0) = 1 - 1 = 0

 At Θ = Π/ 2 ;   Y =

 (1 - Cos Π/ 2) = 1 - 0 = 1

 Now see at Figure 7 for appropriate understanding of concept.

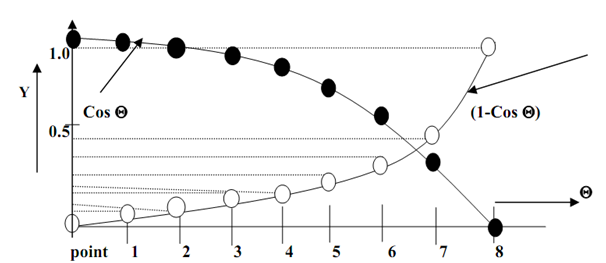
Note: consisting projections of points upon curve, over Y axis, we will obtain a pattern as same to Figure 6 that is required to generate positive acceleration.

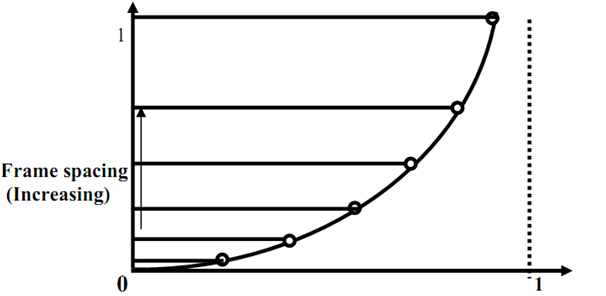
Raises in gap along y-axis depict that spacing among key frames increases that leads to accelerated motion.

As our intend here is to have acceleration in the motion thus we create N-in between frames, among two key frames that leads to N+1 sections and divide Θ axis in to N fragments, for all fragments, we get Y=(1-CosΘ). Substituting diverse values of Θ we find various Y as demonstrated in figure 7 and 7(a), the space among frames is continuously raising, imparting an accelerated motion.

Length of all subintervals (Θ) = (Θ₁-Θ₂ )/no. of subintervals = (Π/ 2 - 0) N + 1 = Π/ 2(N + 1)

Hence, change in (Θ) produces change of 1- Cos ( (Π / 2)(N+1))