Before proceeding along with in fact solving systems of differential equations there's one topic which we require to take a look at. It is a topic that's not at all times taught in a differential equations class as, but if you're in a course where this is taught we must cover it hence you are prepared for this.

Let's begin with a general homogeneous system,

x?  = A x?

See there as,

x?= 0?

It is a solution to the system of differential equations. What we'd want to ask is, perform the other solutions to the system approach such solution as t raises or do they move away from this solution? We did anything the same to this when we classified equilibrium solutions in an earlier section. Actually, what we're doing now is simply an extension of this concept to systems of differential equations.

Here x?= 0? is termed as an equilibrium solution for such system. Since with the single differential equations case, equilibrium solutions are those solutions for that,

A x?= 0?

We are going to suppose that A is a nonsingular matrix and thus will contain only one solution,

x?= 0?

And therefore we will have only one equilibrium solution.

Back in the only differential equation case recall which we started by selecting values of y and plugging these in the function f(y) to find out values of y′. We after that used these values to sketch tangents to the solution at which exact value of y. By this we could sketch in several solutions and use this information to categorize the equilibrium solutions.

We are going to perform something the same now, but this will be slightly different suitably. First we're going to limit ourselves down to the 2x2 case. Thus, we'll be looking at systems of the type,

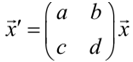
x₁' = ax₁ + bx₂                                                    =>               

x₂' = cx₁ + dx₂

Solutions to such system will be of as,

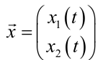
And our only equilibrium solution will be,

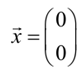
Under the single differential equation case we were capable to sketch the solution, y(t) under the y-t plane and notice actual solutions. Though, this would somewhat not easy in such case as our solutions are actually vectors. What we're going to do now is thing of the solutions to the system as points in the x₁-x₂ plane and plot such points. Our equilibrium solution will correspond to the origin of x₁-x₂plane and the x₁-x₂ plane is termed as the phase plane.

To draw a solution in the phase plane we can select values of t and plug these in the solution. It provides us a point in the x₁-x₂ or phase plane which we can plot. Doing this for various values of t will then provide us a sketch of what the solution will be doing under the phase plane. A sketch of an exact solution in the phase plane is termed as the trajectory of the solution. When first we have the trajectory of a solution sketched we can after that asks whether or not the solution will move toward the equilibrium solution as t rises.

We would want to be capable to sketch trajectories without in fact having solutions in hand. There are a couple of ways to perform this. We'll look at one of those here and we'll look at the other in the next couple of sections.

One way to get a sketch of trajectories is to do something similar to what we did the first time we looked at equilibrium solutions. We can select values of x? but see there that these will be points in the phase plane and calculate A x?. This will give a vector that represents x?' at that exact solution. As with the particular differential equation case that vector will be tangent to the trajectory at such point. We can draw a bunch of the tangent vectors and after that sketch in the trajectories.

It is a fairly work intensive manner of doing these and isn't the manner to perform them in general. Though, this is a way to find trajectories without doing any solution work. All we require is the system of differential equations.