Operation of Algorithm

The following sequence of diagrams shows the operation of Dijkstra's Algorithm. The bold vertices show the vertex to which shortest path has been find out.

Step 1:

Initialize the graph, all of the vertices have infinite costs except the source vertex that has zero cost

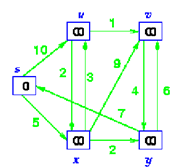
 Step 2

From all the adjacent vertices, select the closest vertex to the source s.

As we initialized d[s] through 0, it's s. (illustrated in bold circle)

Add it to S

Relax all vertices adjacent to s, that means u & x

Update vertices u & x by 10 & 5 as the distance from s.

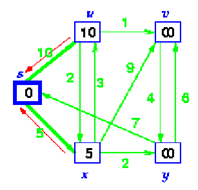
            Step 3:

Select the nearest vertex, x. Relax all of vertices adjacent to x

Update predecessors for u, v & y. Predecessor of x = s

Predecessor of v = x ,s

Predecessor of y = x ,s

add x to S

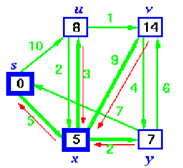
Step 4:

Now y is the closest vertex. Add it to S.

Relax v and adjust its predecessor.

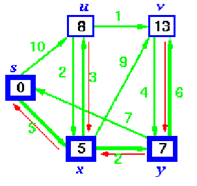
 Step 5:           

u is now closest, add it to S and adjust its adjacent vertex, v.

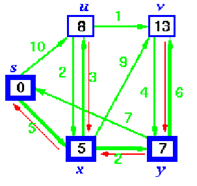
Step 6:

Finally, add v to S.

The predecessor list now defines the shortest path from each node to s.