Finding the number of Permutations of 'n' dissimilar things taken 'r' at a time:
After looking at the definition of permutations, we look at how to evolve a general framework for finding the number of permutations of 'n' dissimilar things taken 'r' at a time. To make this simpler we again go back to our introduction example but with a slight change. Here we consider five units and one has to take four out of five units. Now in how many ways can one take the first unit? Five ways. Since he can take any one of the five units. After taking the first unit in five ways, in how many ways can he take the next unit? Necessarily in four ways. What about the third and the fourth units? He can take them in three and two ways respectively. At this point it is easy to observe the pattern.
Now applying the principle we have studied above can we state that four units out of five can be taken in
5 x 4 x 3 x 2 ways
Yes, we can and this principle forms the basis for finding the number of permutations of n dissimilar things taken r at a time. Therefore, the first thing can be taken in n ways, the second thing can be taken in n - 1 ways, the third thing can be taken in n - 2 ways and in a similar fashion the rth thing can be taken in n - (r - 1) ways. Why n - (r - 1)? Because the first thing is taken in n - (1 - 1) = n ways, the second in n - (2 - 1) = n - 1 ways, .... the rth thing in n - (r - 1) = n - r + 1 ways. From the principle, taking r dissimilar things from n things is therefore
n.(n - 1).(n - 2)............(n - r +1) ways.
What we will get if we have to take all the given things at a time. It will be n.(n - 1).(n - 2).(n - 3)......to n factors. That is,
n.(n - 1).(n - 2).(n - 3)........3.2.1
But this happens to be the definition of n factorial, denoted as n! At this stage only remember that n! = n.(n - 1).(n - 2).(n - 3)..........3.2.1
Taking r things out of n things is denoted by nPr and it stands for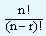 
. On simplifying this, we get
n.(n - 1).(n - 2)............(n - r + 1)
which is taking r things out of n.
(Note: Since selecting 'r' elements from 'n' elements is similar to filling up 'n' positions with 'r' things, we often use this analogy in understanding concepts in Permutations and Combinations.)
Now we take up an example.
Example
There are six boxes and three balls. In how many ways can these three balls be discretely put into these six boxes.
The first ball can be put into any one of the six boxes. That is six ways. The second ball can be then put into any one of the remaining five boxes. That is in five ways and finally the last ball can be put into one of the remaining four boxes, which gives us 4 ways. That is, the three balls can be put into six boxes in
6 x 5 x 4 = 120 ways.
For the same problem let us apply the formula and check whether we get the same answer.
 |
|
|
|
|
|
|
= |
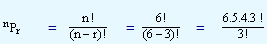120 |
Finding the number of permutations of 'n' things taken 'r' at a time, given that each of the elements can be repeated once, twice .... up to 'r' times:
In this case the first place can be filled up by any one of the n values. The second position can also be filled up by any one of the n values. Similarly the third, fourth and the rth positions. This is because we have the discretion to use each element for as many as r times. Therefore, r things out of n things can be selected in nr ways.
Example
Find the number of ways in which three prizes can be awarded to three students, when each student is eligible for all the prizes?
The first prize can be awarded to any one of the three students. That is, it can be given in three ways. Similarly the second and third prizes. Therefore, the three prizes can be given away in 33 ways, which is 27 ways.
Till now we have been looking at situations where the elements are different from each other. On some occasions we come across situations wherein some elements are of one kind, some other elements are of one kind and the rest all different. In this part we obtain a general framework which helps us to solve problems like these.
To find the number of ways in which n things may be arranged among themselves, taking all at a time, when p of the things are alike (of one kind), q of them alike but of another kind, r of them of a third kind and the rest all different:
We have a total of n things, of which p are of one kind, q are of one kind, r of one kind and the rest that is n - (p + q + r) things being distinct. If nPr is the required number of permutations and then if p things are replaced by same number of distinct things from any one of the nPr permutations without disturbing the position of the remaining letters, we could form p! new permutations. And if this change is carried out in each of the nPr permutations, we will obtain nPr x p! permutations.
If the same procedure is carried out for q and r things, the number of permutations would be nPr x p! x q! x r!. Since the things are all now different, the number of arrangements that can be made among themselves is n!. That is, n! = nPr x p! x q! x r!. This can be expressed as
|
|
=
|
 |
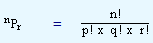which is also our required equation.
Example
You are given a word "MANAGEMENT" and asked to compute the number of permutations that you can form taking all the letters from this word.
We observe that the given word consists of 10 letters in all. In these 10 letters, we find two letters each of M, N, A and E. The two remaining letters are G and T. By applying the above formula, the number of permutations that can be formed by taking all the letters is
|
=
|
 |
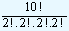Example
There are two sisters among a group of 20 girls. In how many ways can the group be arranged around a circle so that there is exactly one person between the two sisters?
18 sisters can be arranged around a circle in 17! ways. There are exactly 18 places where the two sisters can be arranged. The sisters can be arranged in 2! ways. Therefore, the total number of ways 17! x 2 x18 = 2 x 18!