Motion on the inclined plane when the surface is smooth:

Sol: WHEN THE SURFACE SMOOTH

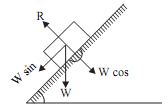
The Figure given shows a body having weight W, sliding down on a smooth inclined plane. Assume,

θ= Angle which is made by inclined plane with horizontal
a = Acceleration of the body

m = Mass of the body = W/g

As the surface is smooth that is frictional force is zero. Hence force acting on body is its own weight W and reaction R of the plane.

The resolved part of W perpendicular to plane is Wcosθ, which is balanced by R, while the resolved part parallel to plane is Wsinθ, which produced acceleration down the plane.

Net force acting on body down the plane

F = W.sinθ  , but F = m.a

m.a = m.g.sinθ

That is,             a = g.sinθ     (For body move down because of self weight.)

and,                   a = -g.sinθ    (For body move up because of some external force)