Midpoint Rule - Approximating Definite Integrals

This is the rule which should be somewhat well-known to you. We will divide the interval [a,b] into n subintervals of equal width that is,

Δx = (b-a) / n

We will indicate each of the intervals like,

 [x₀,x₁],[ x₁,x₂],......, [x_n-1,x_n] where x₀ = a and x_n = b

After that for each interval let x_i* i x be the midpoint of the interval. After that we sketch in rectangles for each subinterval with a height of f (x_i*). At this point there is a graph showing the set up using n=6.

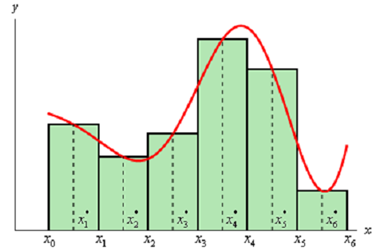
We can simply find out the area for each of these rectangles and thus for a general n we get that,

∫^b_a f(x) dx ≈ Δx f (x₁*) + Δx f (x₂*) + ..... + Δx f (x*_n)

Or, on factoring out a Δx we acquire the general Midpoint Rule.

∫^b_a f(x) dx ≈ Δx [f (x₁*) + f (x₂*) + ..... + f (x_n*)]