Methods of elimination

Example 1 Solve out the given system of equations.

x - 2 y + 3z = 7

2 x + y + z = 4

-3x + 2 y - 2 z = -10

Solution

We will try and find values of x, y, and a z which will satisfy all three equations at the same time.  We are going to utilizes elimination to remove one of the variables from one of the equations & two of the variables from another of the equations. The cause for doing this will be clear once we've in fact done it.

The elimination method in this case will work a bit differently than in two equations.  As with two equations we will multiply as several equations as we have to so that if we start adding up pairs of equations we can eliminate one of the variables.

In this case it seems like if we multiply the second equation by two it will be quite simple to eliminate the y term from the second & third equation by adding the first equation to both of them.  Thus, let's first multiply the second equation by two.

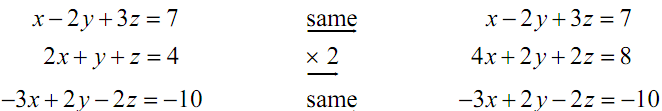
Now, along with this new system we will replace the second equation along with the total of the first & second equations and we will replace the third equation along with the total first and third equations.

Following is the resulting system of equations.

x - 2 y + 3z = 7

5x+ 5z =15

-2 x + z = -3

Thus, we've eliminated one of the variables from two of the equations.  Now we have to eliminate either x or z from either the second equations or third equations. Again, we will utilize elimination to do this. In this we will multiply the third equation by -5 as this will let us to eliminate z from this equation by adding the second onto is.

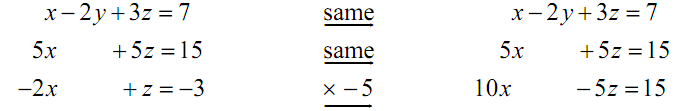
Now, replace the third equation along with the sum of the second equation & third equation.

x - 2 y + 3z = 7

5x+ 5z = 15

15x = 30

Now, at this instance notice that the third equation can be rapidly solved to determine that x = 2 .  Once we know this we can plug it into the second equation and that will give us an equation which we can solve out for z as follows.

5 ( 2) + 5z = 15

10 + 5z = 15

5z = 5

z = 1

At last, we can substitute both x & z into the first equation that we can use to solve for y. Following is that work.

2 - 2 y + 3 (1) = 7

-2 y + 5 = 7

-2 y = 2

y = -1

Hence, the solution to this system is x = 2 , y = -1 and z = 1.

That was a fair amount of work & in this case there was even less work than normal since in each of the case we only had to multiply a single equation to let us to eliminate variables.

In the previous example we did was use the method of elimination till we could start solving for the variables & then just back substitute known values of variables into previous equations to determine the remaining unknown variables.