Mean Value Theorem : Suppose f (x) is a function which satisfies both of the following.

1. f ( x )is continuous on the closed interval [a,b].

2. f ( x ) is differentiable on the open interval (a,b).

Then there is a number c such that a < c < b and

f ′ (c ) = f (b ) - f ( a ) /b - a

                    Or,

f (b ) - f (a ) = f ′ (c ) (b - a )

Note as well that the Mean Value Theorem doesn't tell us what c is. Only it tells us that at least there is one number c that will satisfy the conclusion of the theorem.

Also note that if it weren't for the fact that we required Rolle's Theorem to prove it we could think of Rolle's Theorem as a special case of the Mean Value Theorem.  To illustrates that just suppose that f ( a ) = f (b ) and then the result of the Mean Value Theorem provides the result of Rolle's Theorem.

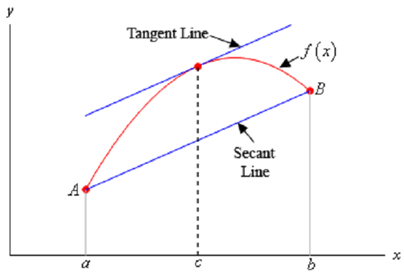
Before we see couple of examples let's think about a geometric interpretation of the Mean Value Theorem.  First define

 A = (a, f ( a )) and B = (b, f (b )) and then we know from the Mean Value theorem that there is a c such that a < c < b and that

 f ′ (c ) = f (b ) - f ( a ) /b - a

 Now, if we draw in the secant line connecting A & B then we can know that the slope of the secant line is,

                         f (b ) - f ( a ) /b - a

Similarly, if we draw in the tangent line to f ( x ) at x = c we know that its slope is f ′ (c ) .

What the Mean Value Theorem described us is that these two slopes have to be equal or in other words the secant line connecting A & B and the tangent line at x = c has to be parallel. We can illustrate this in the following sketch.