Maxima and Minima

We have to make a distinction between relative maxima (or minima) and global maxima (or minima). Let f(x) be a function of x. Then the global maxima of f(x) is the maximum value which f(x) could take for all the possible range of values of x. For example, if x denotes the number of units produced and f(x) denotes the total profit when x units are produced, then we are interested in the maximum value of f(x) for x in the range 0 to the maximum production capacity. Compared to the global maximum, we speak of relative maxima, which is the maximum value of f(x) in a relatively small range of values of x. f(x) is said to have a relative maxima at a point x = a, if the value of the function at a, f(a) is greater than or equal to f(x) for values of x sufficiently close to value a. Look at the graph of a function f(x) given below.

Figure 

This function has a relative maxima at points x = a and at x = c, and a relative minima at points x = b and x = d. If we consider values of x in the range 0 to d, then the global maxima of the function is f(c) attained at point x = c.

The following characteristic features of the relative maxima and minima could be observed:

1. For values of x which are sufficiently close to a(or c), the value of the function first increases and then decreases. The slope of the function is positive up to a(or c) and then it becomes negative. For points b and d, the slope changes from negative to positive.

2. The tangent lines at points a, b, c and d are horizontal indicating that the slopes at those points are zero.

The above observations give the following results:

Result 1:    If f(x) has a relative maxima or minima at  x = a, then the value of the derivative of f(x) at a, 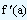  is 0.

Note that the converse may not be true. If at a point a, 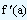   is 0, it need not necessarily imply that f(x) has a relative maxima or minima.

Result 2:    If, at point a, we have 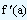   = 0 and  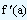  < 0 then f(x) has a relative maxima at x = a.

If 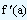  = 0 and  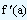  > 0 then f(x) has a relative minima at x = a.

This is because at relative maxima (or minima) the slope changes from positive (or negative) to negative (or positive) for points of close to a.

If 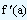  = 0 and  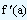  = 0 then we cannot say anything definitely about the occurrence of maxima or minima at point a.

Example 

A manufacturer fixed the following demand curve:

         P(x)   = 200 - 3x

Where x = quantity and P = price

Let the fixed cost of production be Rs.25 and the variable cost Rs.2 per unit. The manufacturer wants to fix the level of output so as to maximize his profit.

The profit function f(x) is:

f(x)    = total revenue - total cost

         = price x quantity - (fixed cost + variable cost)

         = (200 - 3x)x - (25 + 2x)

         = -3x² + 198x - 25

The first order derivative is:

At this level of output, i.e. x = 33, we would like to examine whether we have a minimum or maximum. The second order derivative is:

Therefore,

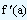< 0

Hence, we conclude that at the level of production of 33 units, the manufacturer will make a maximum profit. The maximum profit is:

-3  *  (33)² + 198  *  33 - 25 = Rs.3,242

Suppose, the quantity that could be produced is limited to the range, say, 10 to 30 units, then we have to check the value of the profit at the boundary points 10 and 30, in addition to any other points in the range (10,30) and then find the optimal level of production.