Magnitude of torque - bending moment:

A prismatic bar of hollow circular cross-section along with outer and inner diameters 100 mm and 80 mm correspondingly, carries a bending moment of 5 kN-m. If the tensile, compressive and shear strengths of the material are given as 140 N/mm², 125 N/mm² and 95 N/mm² respectively, what is the magnitude of torque that may safely be applied in addition to the bending moment.

Solution

Here, the criteria to be considered are as follows:

σ1  › 140 N/mm²

σ2 ›- 125 N/mm²

τ_max   › 95 N/mm²

As the magnitudes of σ1 and σ2 for such bars will be equal, we need to satisfy only.

σ2 ›- 125 N/mm²

and

τ_max   › 95 N/mm²

I for the section π/64(100⁴ -80⁴) = 2.898 × 10⁶ mm⁴

J for the section π/32(100⁴ -80⁴) = 5.796 × 10⁶ mm⁴

Maximum compression due to bending moment,

= - M/I y_max = -5×10⁶× 50/2.898× 10⁶ = - 86.266 N/mm²

If T be the torque applied (in kN-m units), then,

τ_max = T×10⁶×60/5.796×10⁶ = 8.62664 T N/mm²                                          (under torsion alone)

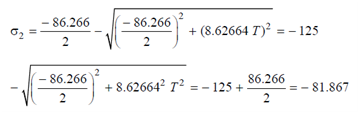
43.133² + 8.62664² T ² = (- 81.867)²

i.e.       T = (81.867² - 43.133²/ 8.62664²)^1/2 =8.066 kN-m

If the applied torque is within 8.066 kN-m, we are certain that the bar will be safe in compression as well as tension.

We should now analyse what torque will have to be applied if τ_max   › 95 N/mm².

We know that 

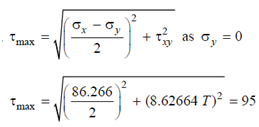
 (under combined bending and torsion)

T= (95² -(86.266/2)²/8.62664²)^1/2 = 9.8119 kN-m

Thus, we cannot apply this much torque, because it will cause compression failure. Therefore, the safe value of additional torque should be restricted to 8.066 kN-m.