In class, we learned that the force on a dipole can be written as F = (p.Δ)E
This force can be used to sort particles with no net charge but with a dipole moment in a method called dielectrophoresis (Google it). This method is often used in biomedical applications to sort particles such as living cells.
Let's work through a problem where we build a dielectrophoresis system.
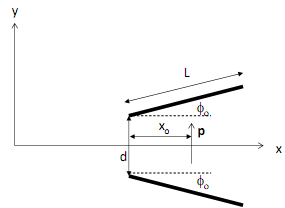
A particle with electric dipole moment p of magnitude 10-25 Ccm, pointing in the y-direction, is placed midway between two large conducting plates at position xo = 5 cm as shown below. Each plate makes a small angle Φo = 1o with respect to the x-axis, with length L=10 cm as indicated, and separated by distance d = 1 mm on the left-hand side.
The top plate is maintained at potential Vo = 1 V and the bottom plate is maintained at zero potential. Assume the plates also extend a distance L = 10 cm in the z-direction.
(a) Calculate an expression for the potential between the plates (ignoring the dipole). Ignore any fringing fields at the edges of the plates. This is the same problem at the end of lab 2.
(b) What is the value of the potential at the centre of the dipole?
(c) Calculate an expression for the electric field between the plates (due to the plates not the dipole).
(d) What is the magnitude and direction of the field at the centre of the dipole?
(e) What is the magnitude and direction of the force on the dipole?
(f) The plates in this problem are to be used in a dielectrophoresis experiment to separate two different particles of mass 10-8 g and 10-10 g, both with the dipole moment p as defined above. If the particles are initially at rest at the position shown in the figure below, how long should one run the experiment to separate the two particles by 1 μm?