Logarithmic form and exponential form ; We'll begin with b = 0 , b ≠ 1. Then we have

y= log_b x          is equivalent to                  x= b ^y

The first one is called logarithmic form and the second is called the exponential form.  Remembering this is the key to evaluating logarithms. The number b, is base.

Example Without a calculator give the precise value of following logarithms.

(a) log2 16 

 (d) log₉ (1/531441) 

(e) log _1/6 36 

Solution

To rapidly evaluate logarithms the simplest thing to do is to convert the logarithm to exponential form.  Hence, let's take a look at the first one.

(a) log₂ 16

Firstly, let's convert to exponential form.

log₂ 16 =?        is equivalent to            2^? = 16

Hence, we're really asking two raised to what gives 16.  As 2 raised to 4 is 16 we get,

log₂ 16 = 4       because            2⁴ =16

We'll not do the remaining parts in fairly this detail, however they were all worked in this way.

 (d) log ₉(1/531441) = -6        because            9^-6  = 1/9⁶  =    1 /531441

 (e) log _1/6 36   = -2      because                        (1/6)^-2=6²=36

Special logarithms

There are a some special logarithms that arise in many places. These are following,

Natural logarithm

                                        ln x = log_e x

This log is called as the natural logarithm

Common logarithm

                                        log x = log₁₀ x

This log is called as the common logarithm

In the natural logarithm the base e is the similar number as in the natural exponential logarithm which we saw in the last section. Given is a sketch of both of these logarithms.

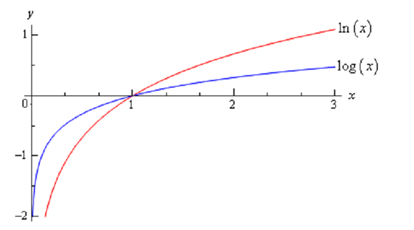
From this graph we get some very nice properties of the natural logarithm which we will use several times in this and later Calculus courses.

ln x → ∞                  as  x → ∞

ln x → -∞             as  x → 0, x > 0