Line Generation Algorithms - Graphic Primitives

In previous section we have discussed the case of frame buffer, here information regarding the image to be projected upon the screen is accumulated in an m*n matrix, in the form of 0s and 1s; the 1s stored in an m* n matrix locations are brightened upon the display and 0's are not brightened on the display and this section that may or may not be brightened is termed as the Pixel i.e. picture element. This information of 0s and 1s offers the needed pattern on the output screen that is for display of information. In that a buffer, the screen is also in the form of m* n matrix, here all sections or niche is a pixel that is we have m* n pixels to constitute the output.

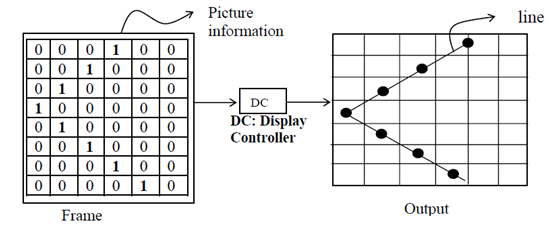
Figure: Basic Line Generation

Here, it is to be noticed that the creation of a line is merely not restricted to the above pattern, since occasionally the line may have a slope and intercept which its information is needed to be stored in more than one part or section of the frame buffer, accordingly in order to draw or to estimated line two or more pixels are to be done ON. Thus, the result of the line information in the frame buffer is exhibited like a stair; this consequence of having two or more pixels ON to approximating a line among two points say A and B is termed as the Staircase effect. The idea is demonstrated below in following figure.

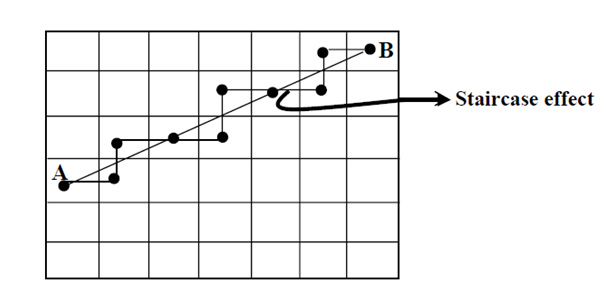
Figure: Staircase effect

Hence, from the above figure, it is clear that while a line to be drawn is simply illustrated by its end points, after that it can be plotted through making close estimates of the pixels that best suit the line, and this estimation is responsible for the staircase consequence, that miss projects the information of the geometry of line accumulated in the frame buffer like a stair. This defect termed as Staircase consequence is prominent in DDA Line generation algorithms, hence, to remove the defect Bresenham line generation Algorithm was initiated. Now we are going to discuss DDA i.e. Digital Differential Analyzer, Algorithm and Bresenham line generation Algorithm next.