Limits At Infinity, Part I : In the earlier section we saw limits which were infinity and now it's time to take a look at limits at infinity.  Through limits at infinity we mean one of the given two limits.

In other terms, we are going to be looking at what happens to a function if we allow x get extremely large in either the +ve or -ve sense. Also, as we'll rapidly see, these limits may also have infinity as a value.

Firstly, let's note that the set of Facts through the Infinite Limit section also hold if the replace the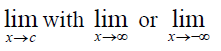   .  The proof of this is closely identical to the proof of the original set of facts along with only minor modifications to manage the change in the limit and hence is left to the reader. Actually, many of the limits that we're going to be looking at we will require the following two facts.

Fact 1

1. If r means to a positive rational number and c means to any real number then,

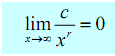
2. If r is a positive rational number, c is any real number and x^r   is explained for x < 0 then,

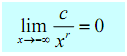
The first part of this fact has to make sense if you think regarding it.  Since we are requiring r > 0 we know that x^r will stay in the denominator.  Next as we enhance x then x^r will also enhance.  So, we have a constant divided by an increasingly large number and hence the result will be increasingly small.  Or, in the limit we will obtain zero.

The second part is closely identical except we require worrying about x^r being explained for negative x. Here, this condition is to avoid cases such as r =  1/2 .  If this r were let then we'd be taking the square root of -ve numbers which would be complex and we desire to avoid that at this level.

Note that the sign of c will not influence the answer.  In spite of of the sign of c still we'll have a constant divided by a very large number that will result in a extremely small number and the larger x get the smaller the fraction gets. The sign of c will influence which direction the fraction approaches zero (i.e. from the positive or negative side) however it still approaches zero.

Let's begin with the examples with one that will lead us to a nice idea which we'll employ on a regular basis regarding limits at infinity for polynomials.