Limit Properties :  The time has almost come for us to in fact compute some limits.  Though, before we do that we will require some properties of limits which will make our life somewhat easier.  Thus, let's take a look at those first. The proof of some properties can be found in the  Proof of several Limit Properties section of the Extras chapter.

Properties

First we will suppose that  exist & that c is any constant. Then,

1.   

     In other terms we can "factor" a multiplicative constant out of limit.

2.   

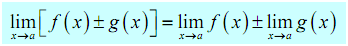
Therefore to take the limit of a sum or difference all we have to do is take the limit of the individual parts & then put them back together along with the appropriate sign. It is also not limited to two functions.  This issue will work no matter how many functions we've got separated through "+" or "-".

3.  

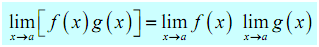
We take the limits of products in the similar way which we can take the limit of sums or differences. Just take the limit of the pieces & then put them back together.  Also, such as with sums or differences, this fact is not restricted to just two functions.

4.

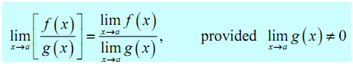
As noted in the statement we only have to worry regarding the limit in the denominator being zero while we do the limit of a quotient.  If it were zero we would end  along with a division by zero error and we have to avoid that.

5. 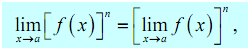  ,  where n refer to any real number

In this case n can be any real number (positive, integer, negative fraction, zero, irrational etc.).  In this case that n refers to an integer this rule can be thought of as an extended case of 3.

For instance assume the case of n = 2.

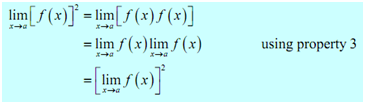
The similar can be done for any integer n.

6.

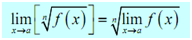
 It is just a special case of the previous example.

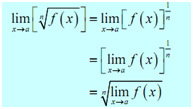
7. 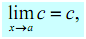    c refer to any real number

In other terms, the limit of a constant is just the constant.  You have to be able to convince yourself of this through drawing the graph of f ( x )= c .

8.

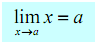
As with the last one you have to be able to convince yourself of this by drawing the graph

of  f (x ) = x .

9.

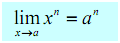
 It is really just a special case of property 5 using f ( x )= x .

Note as well that all these properties also hold for the two one-sided limits in addition to we just didn't write them down along with one sided limits to save on space.

Let's calculate a limit or two using these properties. The next examples will lead us to some really useful facts regarding limits that we will employ on a continual basis.