Before we look at this, let us learn what a multiple is. Take any number say 3. Multiply this number with natural numbers. We obtain 3, 6, 9, 12, 15, 18,.......... The resulting numbers, that is 3, 6, 9, 12, etc. are called multiples of 3. Now to understand the concept of least common multiple consider two numbers 4 and 6. The multiples of 4 and 6 are

Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, ..........

Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, ........

From this we can observe that the common multiples to both 4 and 6 are 12, 24, 36 etc. Of these common multiples the least is 12. This gives our least common multiple as 12. Therefore the least common multiple or LCM is defined as that quantity which is divisible by the quantities of which it is a LCM without a remainder. In our example, 12 is the least possible quantity that can be divided by 4 and 6 without leaving any remainder.

Now, let us take another example and check whether the above method of finding the LCM can be applied to all the problems. Find the LCM of 3, 5 and 7. We list the multiples of these three numbers.

Multiples of 3 = 3, 6, 9, 12, 15, 18, 21, ..............

Multiples of 5 = 5, 10, 15, 20, 25, 30, 35, ..............

Multiples of 7 = 7, 14, 21, 28, 35, 42, 49, ..............

We find that this method takes substantial amount of time. We look at another method given below. This method depends on the premise that most of the numbers can be expressed in terms of prime numbers. That is, if you are given to compute the LCM of numbers 35 and 42, the first thing we do is to express them in terms of prime numbers. That will be

                   35     =     5 x 7

                   42     =     2 x 3 x 7

Since we ought to get a number which is the least common multiple of both these numbers, we choose our prime factors in a manner that the resultant number includes all the prime factors of both the numbers in consideration. But if any prime factor is observed to be common to both the numbers, then it shall be considered only once. Therefore from the prime factors above we choose 5. Observe that 5 is a factor of 35 and not 42. Then we choose 7. Both the numbers have it once, therefore we take it once. 2 is a factor of 42 and not of 35. By the above logic we choose it once. The same with 3 also. Therefore, the product of these numbers gives us 2 x 3 x 5 x 7 = 210 which is our required LCM. Consider another example. Find the LCM of 24 and 45. We express them in terms of prime factors.

                     24      =   2 x 2 x 2 x 3

                     45      =   3 x 3 x 5

From these we know that 2 should be present at least thrice, 3 should be present at least twice and 5 at least once. All these factors multiplied will give us our LCM. It will be 2 x 2 x 2 x 3 x 3 x 5 = 360.

When bigger numbers are given even the above method can prove tedious.

We illustrate another method, which is perhaps more easier than what we have seen above. Compute the LCM of 28, 54 and 81. In this method we write these three numbers as shown below. We start dividing these by an appropriate prime number, which in this case happens to be 2. The quotients are put as shown below. Then we start dividing these quotients by a prime number, this prime number may be the same one which has been already employed or it can be a different prime number (remember that we do not have any rule which specifies that a particular number should be used only for so many times). If all the resultant quotients cannot be divided by a single prime number, then we divide only those quotients that are divisible by the prime number chosen for that step while the non-divisible quotients of that step are retained with the same values. They are carried forward (only to the next step, and this process is repeated until we have prime numbers left in the quotient part which also indicates that we cannot divide these numbers any further. This is shown below.

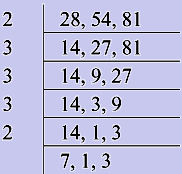
We observe that the quotient part has 7, 1 and 3 which are prime numbers. Now we multiply all the prime numbers with which we divided the given numbers and those which have remained in the last row. That is, 2 x 3 x 3 x 3 x 2 x 7 x 1 x 3  = 2268. Thus our required LCM is 2268.