Interpretations of Definite Integral

There are some quick interpretations of the definite integral which we can give here.

Firstly, one possible interpretation of the definite integral is to give the net area among the graph of f (x) and the x-axis on the interval [a,b].  Therefore, the net area among the graph of

f ( x ) = x² + 1 and the x-axis on [0,2] is,

                                              ∫₀²  x²  + 1dx=14/3

This was the exact area which was given for the initial set of problems that we looked at in this area.

Another interpretation is sometimes called the Net Change Theorem.  This interpretation says that if  f( x ) is some quantity (hence f ′ ( x ) is the rate of change of f ( x) , then,

                                                     ∫_a^b  f ′ ( x ) dx = f (b ) - f ( a )

is the net change in f ( x )on the interval [a,b].  In other terms, calculate the definite integral of a rate of change & you'll obtain the net change in the quantity.  We can illustrates that the value of the definite integral, f (b ) - f ( a ) , does actually give use the net change in f ( x ) and therefore there actually isn't anything to prove with this statement. It is actually just an acknowledgment of what the definite integral of a rate of change tells us.

Therefore as a quick example, if V (t ) is the volume of water within a tank then,

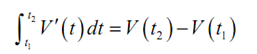
is the total change in the volume as we go from time t₁  to time t₂ .

Similarly, if s (t ) is the function giving the position of some of the object at time t we know that the velocity of the object at any time t is : v (t ) = s′ (t ) . Thus the displacement of the object time t₁  to time t₂ is,

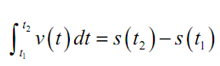
Note as well that in this case if v (t ) is both positive & negative (that means the object moves to both the right & left) in the time frame it will NOT give the net distance traveled.  It will just give the displacement that means the difference amongst where the object started and where it ended up. To obtain the total distance traveled by an object we'd ought to compute,

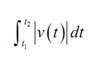
It is significant to note here that the Net Change Theorem only actually makes sense if we're integrating derivative of a function.