Integrals Involving Quadratics

To this point we have seen quite some integrals which involve quadratics.  Example of Integrals Involving Quadratics is as follow:

∫ (x / x² + a) (dx) = ½ 1n |x2 + a| + c

∫ (1/ x² + a²) (dx) = 1/a tan^-1 (x/a)

We as well saw that integrals including  √ (b² x² - a²), √ (a² - b² x²) and √ (a² + b² x²) could be done with a trig substitution.

Notice though that all of these integrals were missing an x term.  They all contain a quadratic term and a constant.

A few integrals including general quadratics are easy enough to do.  For example, the following integral can be done along with a quick substitution.

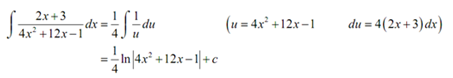
Some integrals along with quadratics can be completed with partial fractions.  For example,

∫ (10x - 6 /( 3x² + 16x+5)) dx

= ∫ ((4/x+5) - (2/3x+1)) dx = 4 1n |x+5| - 2/3 1n |3x+1| + c

Unfortunately, these techniques won't work on a lot of integrals.  A simple substitution will just only work if the numerator is a constant multiple of the derivative of the denominator and partial fractions will only work if the denominator can be factored.