We will begin this chapter by looking at integer exponents.  Actually, initially we will suppose that the exponents are +ve as well. We will look at zero & negative exponents in a bit.

Let's firstly recall the definition of exponentiation along with positive integer exponents.  If a is any number and n is a +ve integer then,

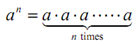
Thus, for example,

                                                 3⁵=3.3.3.3.3 = 243

We have to also employ this opportunity to remind ourselves regarding parenthesis and conventions which we have in regards to exponentiation & parenthesis. It will be specifically important while dealing with negative numbers.  Assume the following two cases.

                       (-2)⁴m                 and            -2⁴

These will contain different values once we appraise them.  While performing exponentiation keep in mind that it is only the quantity which is instantly to the left of the exponent which gets the power.

In the initial case there is a parenthesis instantly to the left so this means that everything within the parenthesis gets the power. Thus, in this case we get,

                                       (-2)⁴ = ( -2) (-2) ( -2) ( -2) = 16

In the second case though, the 2 is instantly to the left of the exponent and thus it is only the 2 that gets the power. The minus sign will stay out in front & will NOT get the power.  In this case we have the following,

                            -2⁴ = - (2⁴ ) = - (2 ⋅ 2 ⋅ 2 ⋅ 2) = - (16) = -16

We put in some added parenthesis to help in illustrate this case. Generally they aren't involved and we would write instead,

                                                         -2⁴  = -2 ⋅ 2 ⋅ 2 ⋅ 2 = -16

The instance of this discussion is to ensure that you pay attention to parenthesis. They are significant and avoiding parenthesis or putting in a set of parenthesis where they don't associate can totally change the answer to a problem.  Be careful.  Also, this warning regarding parenthesis is not just intended for exponents. We will have to be careful with parenthesis during this course.

Now, let's take care of zero exponents & negative integer exponents. In the particular case of zero exponents we have,

                                                                   a⁰ = 1        provided a ≠ 0

Notice down that it is needed that a not be zero. It is important since 0⁰ is not defined.  Here is a rapid example of this property.

                                                 (-1268)⁰ = 1

We contain the following definition for -ve exponents.  If a is any non-zero number & n is a +ve integer (yes, positive) then,

                                                  a^{- n}  =  1 /aⁿ

Can you see why we needed that a not be zero? Keep in mind that division by zero is not described and if we had let a to be zero we would have gotten division by zero.  Here are a couple of rapid examples for this definition,

5^-2  = 1 /5² =  1/25                                             ( -4)^-3  = 1/(-4)³ = 1/-64 =-(1/64)

Here are some main properties of integer exponents. Accompanying each of property will be a rapid example to show its use.  We shall be looking at more complex examples after the properties.