Impulse, Momentum, Work and Energy:

As a part of summary, you can remember various important principles in terms of following equations.

 (i)        Impulse-Momentum equation along a given direction

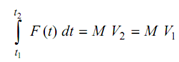
 (ii)       Principle of Conservation of Momentum for a given system of masses M₁, M₂ and M₃.

                     M₁ V₁  + M ₂ V₂  + M ₃ V₃  = M₁ V₁′ + M ₂ V₂′ + M ₃ V₃′

 (iii)      Principle of Conservation of Energy

             (a) In case of Conservative-field

    Total Energy content under any position of all the masses in the system is constant.             

     Considering any two points (1) and (2)

                         ∴ PE (1) + KE (1) = PE (2) + KE (2)

               (b) In case of Non-conservative-field

  ∴ PE (1) + KE (1) = PE (2) + KE (2) + Energy lost during movement from   position (1) to (2).

     (iv)  Work Energy Principle on a given mass M

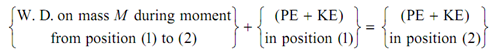
   (v)     Perfectly Elastic Impact

e = Velocityof Departure/ Velocityof Approach

       = (V₂′ - V₁′) / V₁ - V₂ = 1

M ₁ V₁  + M ₂ V₂  = M ₁ V₁′ + M ₂ V₂′ = (m₁  + m₂ ) V_c

There is no loss of energy throughout perfectly Elastic Impact.

 (vi) Perfectly Plastic Impact

        e = 0                        ∴ V₂′ = V₁′ = V_c

            (m₁  + m₂ ) V_c  = m₁ V₁  + m₂  V₂

Energy is lost due to permanent deformation caused by impulsive forces.

E_lost  = m₁ m₂  (V₁ - V₂ )² /2 (m₁ + m₂ )

A large number of examples are solved at the end of most of the important articles so that the application of above referred principles is correctly understood.