By using n = 4 and all three rules to approximate the value of the following integral.

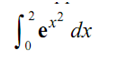
Solution

Very firstly, for reference purposes, Maple provides the following value for this integral.

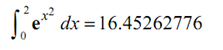
In every case the width of the subintervals will be,

Δx = (2 - 0) /4

= 1/2

and thus the subintervals will be,

[0, 0.5], [0.5, 1], [1, 1.5], [1.5, 2]

Let's endure each of the methods.

Midpoint Rule

∫²₀ e^x2 dx ≈ ½ (e^(0.25)2 +e^(0.75)2  + e^(1.25)2 + e^(1.75)2 ) = 14.48561253

Just keep in mind that we evaluate at the midpoints of each of the subintervals here! The Midpoint Rule occur an error of 1.96701523.

Trapezoid Rule

∫²₀ e^x2 dx ≈ (1/2) / 2 (e⁽⁰⁾² + 2e^(0.5)2  + 2e⁽¹⁾² + 2e^(1.5)2 + e⁽²⁾²) =  20.64455905

The Trapezoid Rule consist an error of 4.19193129

Simpson's Rule

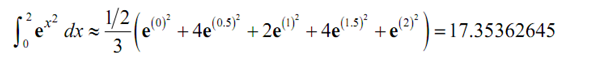
∫²₀ e^x2 dx ≈ (1/2) / 3 (e⁽⁰⁾² + 4e^(0.5)2  + 2e⁽¹⁾² + 4e^(1.5)2 + e⁽²⁾²) =  17.35362645

The Simpson's Rule has an error of 0.90099869.

Not any of the estimations in the previous instance are all that good. The good approximation in this case is from the Simpson's Rule and yet it still had an error of almost 1. To get a better estimation we would require to make use of a larger n.  Thus, for completeness sake here are the estimates for a few larger value of n.

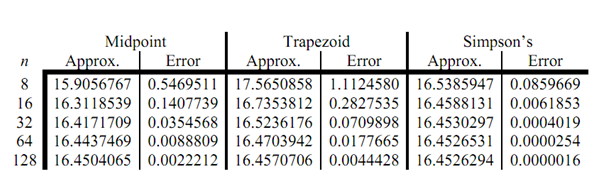
In this type of case we were able to ascertain the error for each estimate as we could get our hands on the exact value.  Frequently this won't be the case and so we'd next like to look at error bounds for every estimate.

These bounds will provide the largest possible error in the estimate, but it should as well be indicated that the actual error may be significantly smaller than the bound. The bound is just only there thus we can say that we know the actual error will be less as compared to the bound.

So, suppose that |f" (x)| < K and |f⁽⁴⁾ (x)| < ((K (b-a)³) / 12n² ) |E_s| <  ((M (b-a)⁵) / 180n⁴⁾