Illustration of a Clipping window ABCD is placed as follows:

A (100, 10), B (160, 10, C (160, 40), D (100, 40)

By using Sutherland-Cohen clipping algorithm determine the visible portion of the line segments i.e. EF, GH and P₁P₂. E (50, 0), F (70, 80), G (120, 20), H (140, 80), P₁ (120, 5), P₂(180, 30).

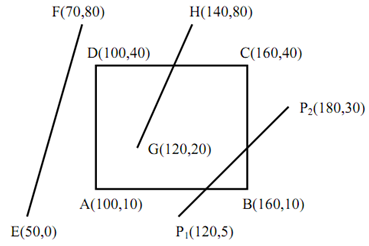
Figure: Example of Cohen Sutherland Line Clipping

At first identifying the line P₁P₂

INPUT: P₁(120, 5),   P₂(180, 30)

x_L = 100,   x_R = 160,    y_B = 10,    y_T = 40

x₁  > x_L then bit 1 of code -P₁ = 0 C_{1 left} = 0

x₁  < x_R then bit 2 of code -P₁ = 0 C_{1 right} = 0

y₁ < y_B then bit 3 of code -P₁ = 1 C_{1 bottom} = 1

 y₁  < y_T then bit 4 of code -P₁ = 0 C_{1 top} = 0

code -P₁ = 0100,

x₂  > x_L then bit 1 of code -P₁ = 0 C_{2 left} = 0

x₂  > x_R  then bit 2 of code -P₁ = 1 C_{2 right} = 1

 y₂  > y _B then bit 3 of code -P₁ = 0 C_{2 bottom} = 0

y₂  < y_T then bit 4 of code -P₁ = 0 C_{2 top} = 0

 code -P₂ = 0010.

Both code -P₁ <> 0 and code -P₂ <> 0

then P₁P₂ not totally visible

code -P₁ AND code -P₂ = 0000

therefore (code -P₁ AND code -P₂ = 0)

then line is not fully invisible.

As code -P <> 0

for  i = 1

{

C_{1 left} (= 0) <> 1 then nothing is done. i = i + 1 = 2

}

code -P₁ <> 0 and code -P₂ <> 0

then P₁P₂ not totally visible.

code -P₁ AND code -P₂ = 0000

therefore (code -P₁ AND code -P₂ = 0)

then line is not fully invisible.

 for   i = 2

     {

C_{1 right} (= 0) <> 1 then nothing is to be done. i = i + 1 = 2 + 1 = 3

}

code -P₁ <> 0 and code -P₂ <> 0 then P₁P₂ not totally visible.

code -P₁ AND code -P₂ = 0000

therefore, (code -P₁ AND code -P₂ = 0)

then the line is not fully invisible.

 for   i = 3

{

 C_{1 bottom} = 1 then find intersection of P₁P₂ with bottom edge y_B = 10

x_B = (180-120)(10-5)/(30-5) + 120

=132

then P₁ = (132,10)

 x₁  > x_L then bit 1 of code -P₁ = 0   C₁ left = 0

x₁  < x_R then bit 2 of code -P₁ = 0   C₁ right = 0

y₁  = y_B then bit 3 of code -P₁ = 0   C₁ bottom = 0

y₁  < y_T then bit 4 of code -P₁ = 0   C₁ top = 0

code -P₁ = 0000

i = i + 1 = 3 + 1 = 4

}

code -P₁ <> 0 but code -P₂ <> 0

then P₁P₂ not totally visible.

code -P₁ AND code -P₂ = 0000

therefore, (code -P₁ AND code -P₂ = 0)

then line is not fully invisible.

As code -P₁ = 0

Swap P₁ and P₂ along with the respective flags

P₁ = (180, 30) P₂ = (132, 10) code -P₁ = 0010 code -P₂ = 0000

C₁ left = 0                         C₂ left = 0

C₁ right = 1                       C₂ right = 0

C₁ bottom = 0                  C₂ bottom = 0

C₁ top = 0                         C₂ top = 0

Reset i = 1

for i = 1

{

C_{1 left} (= 0) <> 1 then nothing is to be done. i = i + 1 = 1 + 1 = 2

}

code -P₁ <> 0, and code -P₂ <> 0

then P₁P₂ is not totally visible.

code -P₁ AND code -P₂ = 0000

therefore, (code -P₁ AND code -P₂ = 0)

then line is not fully invisible.

 for i = 2

{

 C_{1 right}   = 1 then find out intersection of P₁P₂ with right edge x_R = 160

y_R = (30 - 5)(160 - 120)/(180 - 120) + 5

= 21.667

= 22 then P₁ = (160, 22)

 x₁  > x_L then bit 1 of code -P1 = 0   C1 left = 0

x₁  = x_R then bit 2 of code -P1 = 0   C1 right = 0

y₁  > y_B then bit 3 of code -P1 = 0   C1 bottom = 0

y₁  < y_T then bit 4 of code -P1 = 0   C1 top = 0

 code -P₁ = 0000, i = i + 1 = 2 + 1 = 3

}

As both code -P₁ = 0 and code -P₂ = 0 then the line segment P₁P₂ is completely visible.

Consequently, the visible portion of input line P₁P₂ is P'₁P'₂ where, P₁ = (160, 22) and

P₂ = (132, 10).

For the line EF

1)      The endpoint codes are allocated code:

code - E → 0101

code - F → 1001

2) Flags are allocated for the two endpoints:

E_left = 1 (as x coordinate of E is less than xL)

E_right = 0,  E_top = 0 and E_bottom = 1

As the same,

F_left = 1,  F_right = 0,  F_top = 1 and F_bottom = 0

3) Because codes of E and F are both not equivalent to zero the line is not wholly visible.

4) Logical intersection of codes of E and F is not equivalent to zero. Consequently, we may avoid EF line and declare it as wholly invisible.

Identifying the line GH:

a) The endpoint codes are allocated:

code - G → 0000 and

code - H → 1000

b)   Flags are allocated for the two endpoints:

G_left = 0,  G_right = 0,  G_top = 0 and G_bottom = 0.

As the same,

H_left = 0,  H_right = 0,  H_top = 1 and  H_bottom = 0.

c) Because, codes of G and H are both not equivalent to zero according to the line is not totally visible.

d)   Logical intersection of codes of G and H is equivalent to zero consequently we cannot specify it as completely invisible.

f)   Because, code - G = 0, Swap G and H with their flags and set i = 1

Implying   G_left = 0,  G_right = 0,  G_top = 1 and  G_bottom = 0.

H_left = 0,  H_right = 0,  H_top = 0 and  H_bottom = 0.

The same as G → 1000 and H → 0000

6) Because, code - G <> 0 then

for i = 1,

{since G_left = 0

i = i + 1 = 2

go to 3

}

The conditions 3 and 4 don't hold and so we can't declare line GH as completely visible or invisible.

for i = 2, {since G_right = 0

i = i + 1 = 3

go to 3

}

The conditions 3 and 4 don't hold and so we can't declare line GH as completely visible or invisible.

for i = 3, {since Gbottom = 0

i = i + 1 = 4

go to 3

}

The conditions 3 and 4 don't hold and so we can't declare line GH as completely visible or invisible.

for i = 4, {since G_top = 1

Intersection along with top edge, as P(x, y) is found as given below:

Any of line passing via the points G, H and a point P(x, y) is given via y - 20 = {(180 - 20) /(140 - 120)}(x - 120) or, y - 20 = 3x - 360 or, y - 30 = -340

Because, the y coordinate of every point on line CD is 40, consequently we put y = 40 for the point of intersection P(x, y) of line GH along with edge CD.

40 - 3x = -340 or, - 3x = - 380

Or else x = 380/3 = 126.66 ≈ 127

Consequently, the point of intersection is P (127, 40). We allocate code to it.

Because, the point lays on edge of the rectangle hence the code allocated to it is 0000. Here, we allocate G = (127, 40); i = 4 + 1 = 5. State 3 and 4 are again checked. Because, codes G and H are both are equivalent to 0, hence, the line among H(120, 20) and G(127, 40) is wholly visible.