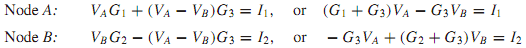Q. Illustrate Nodal-Voltage Method ?
A set of node-voltage variables that implicitly satisfy the KVL equations is selected in order to formulate circuit equations in this nodal method of analysis. A reference (datum) node is chosen arbitrarily based on convenience, and from each of the remaining nodes to the reference node, the voltage drops are defined as node-voltage variables. The circuit is then described completely by the necessary number of KCL equations whose solution yields the unknown nodal voltages from which the voltage and the current in every circuit element can be determined. Thus, the number of simultaneous equations to be solved will be equal to one less than the number of network nodes. All voltage sources in series with resistances are replaced by equivalent current sources with conductances in parallel. In general, resistances may be replaced by their corresponding conductances for convenience.Note that the nodal-voltagemethod is a generalmethod of network analysis that can be applied to any network.
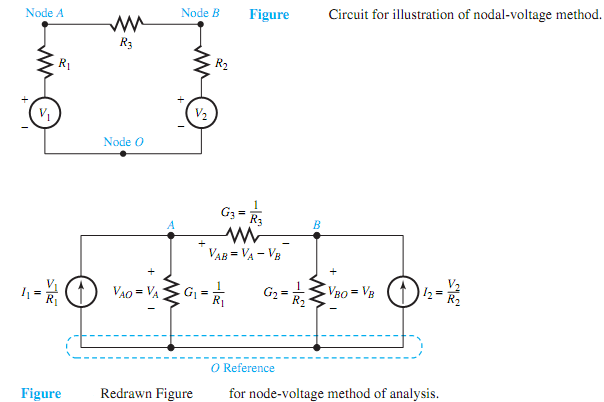
Let us illustrate the method by considering the simple, but typical, example shown in Figure 2.2.1. By replacing the voltage sources with series resistances by their equivalent current sources with shunt conductances, Figure 2.2.1 is redrawn as Figure 2.2.2, in which one can identify three nodes, A, B, and O.
Notice that the voltages VAO, VBO, and VAB satisfy the KVL relation:
VAB + VBO - VAO = 0, or VAB = VAO - VBO = VA - VB
where the node voltages VA and VB are the voltage drops from A to O and B to O, respectively. With node O as reference, and with VA and VB as the node-voltage unknown variables, one can write the two independent KCL equations: