The digital circuits that we use now-a-days are constructed with NOR or NAND gates in place of AND-OR-NOT gates. NOR & NAND gates are known as Universal Gates as we can realize any digital system with these gates. To prove this point we are required to only show the basic gates: AND, OR & NOT may be realized with either just NAND or with just NOR gate. This is displayed in figure below:

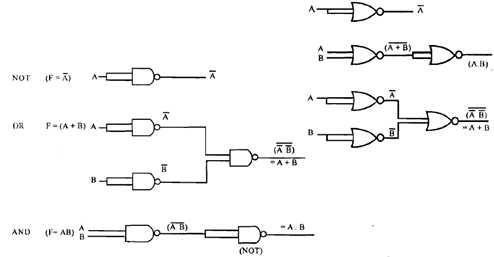
Figure:  Basic Logic Operations with NAND and NOR gates

Any Boolean expression can be realized with NAND gates by realizing function in sum of product form.

Illustration: Consider function F (A, B, C) = Σ (1,2,3,4,5,7). Initially bring it in SOP form. So from K-Map displayed in figure (a) we find

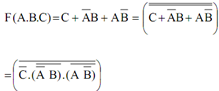
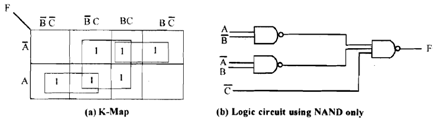
Figure: K-Map & Logic circuit for function F (A, B, C) = Σ (1,2,3,4,5,7).

In the same way any Boolean expression can be realized with just NOR gate by implementing in POS form. Let's take similar illustration F (A, B, C) =Σ (1,2,3,4,5,7).  

The above function F can be expressed in POS form as  below:

F (A, B, C) = ∏ (0,6)

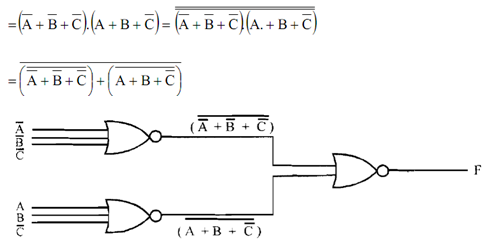
Figure: Logic circuit for function F (A, B, C) = Σ  (1,2,3,4,5,7) using NOR gates