Next, let us consider the case of a balanced delta-connected load with impedance of 5 45° supplied by a three-phase, three-wire 100-V system, as shown in Figure (a). We shall determine the line currents and draw the corresponding phasor diagram. With the assumed positive phase sequence (A-B-C) and with ¯V_BC as the reference phasor, the line-to-line voltages ¯V_AB, ¯V_BC, and ¯V_CA are shown in Figure. The rms value of the line-to-line voltages is 100 V for our example. Choosing the positive directions of the line and phase currents as in Figure(a), we have

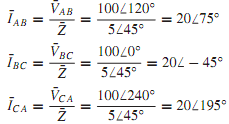
By the application of Kirchhoff's current law at each of the vertices of the delta-connected load, we obtain

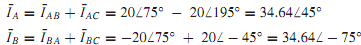
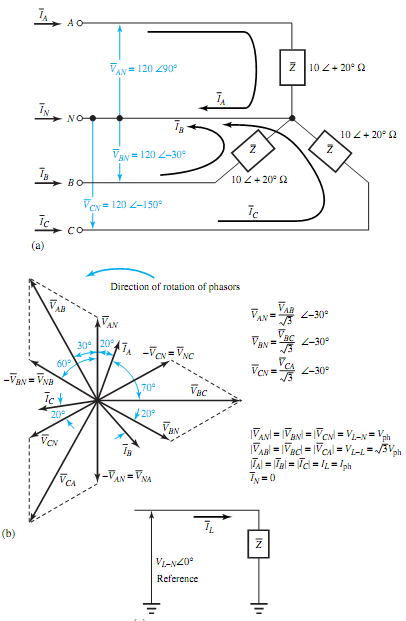
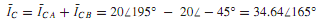
The phasor diagram showing the line-to-line voltages, phase currents, and line currents is drawn in Figure(b). The load power factor is lagging, and is given by cos 45°. For a balanced delta-connected load, the phase voltages and the line-to-line voltages are equal in magnitude, and the line voltages are in phase with the corresponding phase voltages.

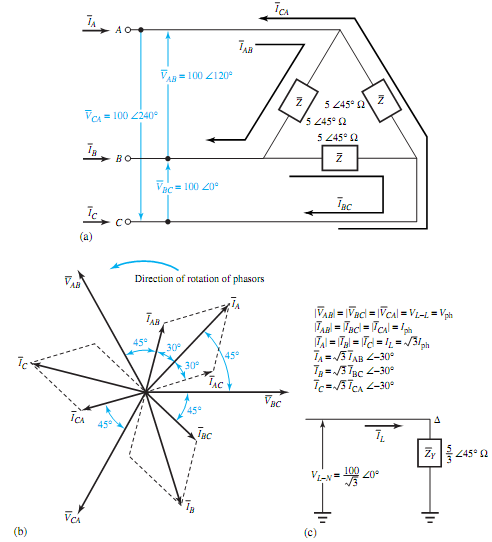
The line currents, in magnitude, are √3 times the phase currents, and the phase currents lead the corresponding line currents by 30°. The preceding example can also be solved by the one-line equivalent method for which the delta-connected load is replaced by its equivalent wye-connected load. The single-line equivalent circuit is shown in Figure(c). The details are left as an exercise for the student.