A politician claims that the mean salary for managers in his state is more than national mean $82,000.  The salaries (in dollars) for a random sample of 30 managers in the state are listed. At α = 0.07, is there enough evidence to support the claim?

86,809	72290	81862	79764	79511	75716	72039	83358	90425	95658
85221	72387	85468	76680	76529	98304	97118	74618	90788	83777
99303	92608	79489	72045	79296	90872	72865	82948	84042	93539

Solution:

a) Identification of Null and alternative hypotheses:

Null hypothesis:

H₀ The mean salary for managers in the state is not more than $82000

H₀  µ ≤ 82000

alternative hypothesis:

H₀  The mean salary for managers in the state is more than $82000

H₀  µ > 82000

Level of significance (α) = 0.07                         One tailed test

Assumptions:

Population is normally distributed.

Data Information: In the above data we find

n (Sample size) =  30

σ (Population standard deviation)   = 8315.90

 X‾ (Sample mean) = 83410.97

b) Calculation of Test Statistic:

 

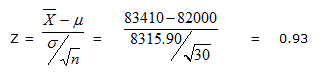
c) Finding P value

 

P value   = P (Z > Z observed)

             = P (Z > 0.93)

             = 1 - P(Z < 0.93)

             = 1- 0.8238

             = 0.1762   

d) Decision Rule:

 Reject H₀ if P value is less than the level of significance.

Decision:

Since P value (observed level of significance) = 0.1762 is greater than α (level of significance) = 0.07, we fail to reject H₀.

Posted Date: 3/16/2013 3:09:55 AM | Location : United States

Ask an Expert

Related Discussions:- Identification of null and alternative hypotheses, Assignment Help, Ask Question on Identification of null and alternative hypotheses, Get Answer, Expert's Help, Identification of null and alternative hypotheses Discussions

Write discussion on Identification of null and alternative hypotheses
Your posts are moderated

Write your message here..

Related Questions

Dist4ibution, I want support about statistical distributions I want support about statistical distributions

In-depth analysis of the effects of the salary, Background: There was no 2... Background: There was no 2004-05 National Hockey Leagues (NHL) season because of a labour dispute between the players and the teams. One of the outcomes of the labour dispute was

Qualitative description of a report, report report

Permutation, Find the number of different ways in which the 9 letters of th... Find the number of different ways in which the 9 letters of the word GREENGAGE can be arranged if exactly two Gs are next to each other?

Factor anaylsis statistical method , First of all, thank you very much for ... First of all, thank you very much for your help. I have a mixes data base, categorial variable, liclekt scale on 5 and 4, and continous variable, and several dummy. I would need h

The value of its common stock, The Washington Corp stock has a β of 1.15 an... The Washington Corp stock has a β of 1.15 and it will pay a dividend of $2.50 next year. The expected rate of return of the market is 17% and the current riskless rate is 9%. The e

Index number, Limitations of ndex numbers Limitations of ndex numbers

T TEST and chi square test, Course of Study MBA 10% B.Tech 90% BBA 0% Diplo... Course of Study MBA 10% B.Tech 90% BBA 0% Diploma 0% Annual College Fee 25,000-30,000 0% 40,000-50,000 10% 85,000-90,000 90% 90,000 Above 0% Taken an Education Loan Yes 100

Bad debt reserve, Explain definition of bad debt reserve and provision in t... Explain definition of bad debt reserve and provision in terms of accounts receivable likely to be uncollected. Bad debt reserve provision Bad debt reserve provision is a amount

Joint probability, Two construction contracts are to be randomly assigned t... Two construction contracts are to be randomly assigned to one or more of three firms. Numbering the firms I, II, and III, let X1 be the number of contracts assigned to firm I, and