Q. How to Subtract fractions with different denominators?

Ans.

As with adding fractions, you can't subtract unless the denominators are the same. Here is an example:

9/10 - 1/2

Step 1: Factor the denominators.

9/2.5 - 1/2

Step 2. Notice what the differences are. The one on the left has two factors, 2 and 5. The one on the right has a single factor of 2.

Step 3: Figure out what extra factors are needed to make the denominators equal. If the right-hand denominator had a factor of 5, then they would be equal.

Step 4. Put in the extra factors. (Be sure to put them both in the numerator and denominator!) Here, we'll put the extra 5 factor in the right-hand fraction, both top and bottom:

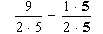
Remember, this is allowed, because multiplying the numerator and denominator of a fraction by the same number doesn't change the value of the fraction.

Step 5. Now the denominators are the same, and you can subtract. You can simplify the numerators, but don't simplify the denominators yet!

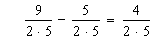
Step 6. Reduce (simplify). Since you have not simplified the denominators yet, it's easy to see the factors of 2 and 5 on the bottom. You know that 2 is a factor of 4, so you can cancel out a 2:

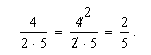
And that's all there is to it!