Also, as x obtain very large, both positive & negative, the graph approaches the line specified by y = 0 .   This line is called a horizontal asymptote.

Following are the general definitions of the two asymptotes.

1.   The line x = a is vertical asymptote if the graph rise or fall without bound on one or both sides of the line as x moves in closer & closer to x = a .

2.   The line y = b is horizontal asymptote if the graph approaches y = b as x increases or decreases without bound.  Note that it doesn't have to approach y = b as x BOTH increases and decreases.  Only it needs to approach it on one side in order for it to be a horizontal asymptote.

Determining asymptotes is in fact a fairly simple procedure. First, let's begin with the rational function,

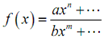
where n refer to the largest exponent in the numerator and m refer to the largest exponent in the denominator.

Then we have the given facts regarding asymptotes.

1.   The graph will have vertical asymptote at x = a if the value of denominator is zero at x = a and the numerator isn't zero at x = a .

2.   If n < m then the x-axis is the horizontal asymptote.

3.   If n = m then the line y = a/ b is the horizontal asymptote.

4.   If n > m there will be no horizontal asymptotes.

The procedure for graphing a rational function is somewhat simple. Following it is.