The BBC hosts a homophone quiz on its website; your task for this lab is to develop an automatic method for completing the quiz, with the aim being to get as high a score as possible. Since this is the fourth lab, and you have no doubt become language processing experts, we have chosen the advanced quiz!

The questions are as follows (the blank indicates the position of the disputed word, and the words appearing in brackets at the end are the possible options).

1. I don't know to go out or not (weather/whether)

2. Houses were being built on this (site/sight)

3. We went the door to get inside (through/threw)

4. I really want a car (new/knew)

5. They all had a of the cake (piece/peace)

6. She had to go to prove she was innocent (caught/court)

7. We were only to visit at certain times (allowed/aloud)

8. We had to a car while we were on holiday (hire/higher)

9. Tip the jug and lots of cream on the strawberries (poor/pour/paw)

10. She went back to she had locked the door (check/cheque)

For the purposes of this exercise, you will use a simple language model to estimate the probability that each of the candidate words is correct. To do this you will need to compute the frequency of each of the words in a large corpus. Additionally you will need a count of all bigrams (two word sequences) in the corpus. Using nltk this becomes trivial. For this lab we will be using the entire Brown corpus to get these counts.

1 Unigram Model

The first part of this lab is to use a very simple model to select the word which goes in the blank: simply pick the most frequent word (using the unigram frequencies above). You should write a Python program to read in the sample sentences available.

Your program should then output for every sentence the candidate word it thinks should go in the blank.

2 Bigram Model

The second method you should attempt is to make use of the bigram counts to determine which of the potential candidates makes the whole sentence more probable (i.e. you should develop a basic language model). If one is willing to make certain assumptions, the probability of a sequence of words w1,w2,w3,. . .,wn is given by:

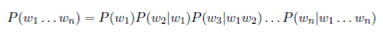
When using a bigram language model, we approximate the above probability with using only the previous word:

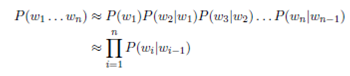
You should think about the entire calculation you need to make, and which parts of it are common to all possible choices in the blank space for the homophone disambiguation task.

We estimate the bigram probabilities in the equation above using counts from a large corpus.

The standard way to estimate bigram probabilities is:

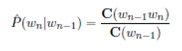
3 Smoothing

Results for the task can be improved using smoothing. Implement the "Plus One Bi-gram

Smoothing" that was described in lecture. The bigram probabilities are estimated as:

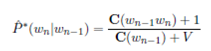
where V is the number of distinct words in the training corpus (i.e. the number of word types).

4 Hand-in

Hand in four files:

1. A Python program called lab4a.py that reads on standard input a file of sentences in the format of the test file supplied and outputs on standard output one word per line, where the word on the k-th line is that homophone from the pair of homophones at the end of the k-th input sentence which the unigram model (section 1 above) predicts as the most probable to fill in the blank in the k-th input sentence.

2. A Python program called lab4b.py which is the same as lab4a.py, except that the words proposed should be the homophones deemed most probable by the bigram model (section 2 above).

3. A Python program called lab4c.py which is the same as lab4b.py, except that the words proposed should be the homophones deemed most probable by the bigram model with plus-one smoothing (section 3 above).

4. A brief report (maximum 1 side of A4 - half a side is fine) called lab4-report (.doc or.pdf) that:

_ Describes how your programs work and reports the result for each.

_ Discusses why you get the results you get.