If a, b and c are in harmonic progression with b as their harmonic mean then,

b

=

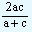This is obtained as follows. Since a, b and c are in harmonic progression, 1/a, 1/b and 1/c are in arithmetic progression. Then,

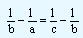
This can be written as

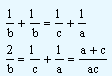
On cross multiplication we obtain

         2ac=b(a + c)

That is, b

=

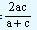The second proposition we are going to look at in this part is: If A, G and H are the arithmetic, geometric and harmonic means respectively between two given quantities a and b then G² = AH. The explanation is given below.

We know that the arithmetic mean of a and b is 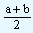  and it is given that this equals to A.

Similarly G2 = ab and H  =

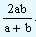The product of AH =

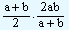= ab. This we observe is equal to G2.

That is, G² = AH, which says that G is the geometric mean between A and H.

Example 1.5.12

Insert two harmonic means between 4 and 12.

We convert these numbers into A.P. They will be 1/4 and 1/12. Including the two arithmetic means we have four terms in all. We are given the first and the fourth terms. Thus,

         T₀      =       a = 1/4 and

         T₄      =       a + 3d = 1/12

Substituting the value of a = 1/4 in T₄, we have 

         1/4 + 3d     = 1/12

         3d             = 1/12 - 1/4 = - 1/6

         d               = -1/18

Using the values of a and d, we obtain T₂ and T₃.

         T₂      =       a + d = 1/4 + (-1/18)

                                     = 1/4 - 1/18 = 7/36

         T₃      =       a + 2d =  1/4 + 2.(-1/18)

                                      =  1/4 - 2/18

                                      =  1/4 - 1/9

                                      =   5/36

The reciprocals of these two terms are 36/7 and 36/5.

Therefore, the harmonic series after the insertion of two means will be 4, 36/7, 36/5 and 12.